摘要:如图.四边形ABCD中.AB=AD.CB=CD.但ADCD.我们称这样的四边形为“半菱形 .小明说“`半菱形’的面积等于两条对角线乘积的一半 .他的说法正确吗?请你判断并证明你的结论.
网址:http://m.1010jiajiao.com/timu_id_730928[举报]
本题中有两小题,请你任选一题作答.
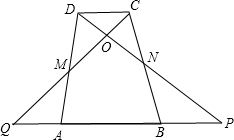
(1)如图,AB∥DC,M和N分别是AD和BC的中点,如果四边形ABCD的面积为24cm2,那么S△QPO-S△CDO= .
(2)若a>3,则
+
= .
 查看习题详情和答案>>
查看习题详情和答案>>
(1)如图,AB∥DC,M和N分别是AD和BC的中点,如果四边形ABCD的面积为24cm2,那么S△QPO-S△CDO=
(2)若a>3,则
| a2-4a+4 |
| 9-6a+a2 |
 查看习题详情和答案>>
查看习题详情和答案>>
梯形ABCD中,DC∥AB,DE⊥AB于点E.
阅读理解:
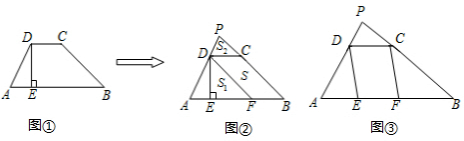
在图①中,延长梯形ABCD的两腰AD、BC交于点P,过点D作DF∥CB交AB于点F,得到图②;四边形BCDF的面积为S,△ADF的面积S1,△PDC的面积S2.
解决问题:
(1)在图②中,若DC=2,AB=8,DE=3,则S=
=
(2)在图②中,若AB=a,DC=b,DE=h,则
=
拓展应用:
如图③,现有地块△PAB需进行美化,□DEFC的四个顶点在△PAB的三边上,且种植茉莉;若△PDC、△ADE、△CFB的面积分别为2m2、3m2、5m2且种植月季.1m2茉莉的成本是120元,1m2月季的成本是80元.试利用(2)中的结论求□DEFC的面积.并求美化后的总成本是多少?
查看习题详情和答案>>
阅读理解:
在图①中,延长梯形ABCD的两腰AD、BC交于点P,过点D作DF∥CB交AB于点F,得到图②;四边形BCDF的面积为S,△ADF的面积S1,△PDC的面积S2.
解决问题:
(1)在图②中,若DC=2,AB=8,DE=3,则S=
6
6
,S1=9
9
,S2=1
1
,则| S2 |
| S1S2 |
4
4
;(2)在图②中,若AB=a,DC=b,DE=h,则
| S2 |
| S1S2 |
4
4
,并写出理由;拓展应用:
如图③,现有地块△PAB需进行美化,□DEFC的四个顶点在△PAB的三边上,且种植茉莉;若△PDC、△ADE、△CFB的面积分别为2m2、3m2、5m2且种植月季.1m2茉莉的成本是120元,1m2月季的成本是80元.试利用(2)中的结论求□DEFC的面积.并求美化后的总成本是多少?

(本题8分)如图,在平行四边形ABCD中,∠D=60°,以AB为直径作⊙O,已知AB=10,AD=m.
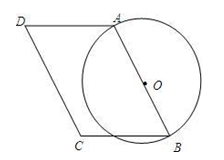
1.(1)求O到CD的距离(用含m的代数式表示);
2.(2)若m=6,通过计算判断⊙O与CD的位置关系;
3.(3)若⊙O与线段CD有两个公共点,求m的取值范围.
查看习题详情和答案>>
