摘要：(1)求证:四边形是正方形,
网址：http://m.1010jiajiao.com/timu_id_728563[举报]
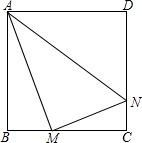正方形ABCD边长为4，M、N分别是BC、CD上的两个动点，当M点在BC上运动时，保持AM和MN垂直．（1）证明：Rt△ABM∽Rt△MCN；
（2）设BM=x，梯形ABCN的面积为y，求y与x之间的函数关系式；当M点运动到什么位置时，四边形ABCN的面积最大，并求出最大面积；
（3）当M点运动到什么位置时Rt△ABM∽Rt△AMN，求此时x的值． 查看习题详情和答案>>
四边形ABCD是正方形．
（1）如图1，点G是BC边上任意一点（不与B、C两点重合），连接AG，作BF⊥AG于点F，DE⊥AG于点E．求证：△ABF≌△DAE；
（2）在（1）中，线段EF与AF、BF的等量关系是 （直接写出结论即可，不需要证明）；
（3）如图2，点G是CD边上任意一点（不与C、D两点重合），连接AG，作BF⊥AG于点F，DE⊥AG于点E．那么图中全等三角形是 ，线段EF与AF、BF的等量关系是 （直接写出结论即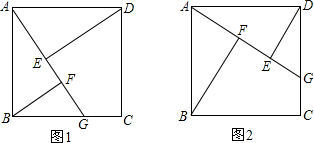
可，不需要证明）．
查看习题详情和答案>>
（1）如图1，点G是BC边上任意一点（不与B、C两点重合），连接AG，作BF⊥AG于点F，DE⊥AG于点E．求证：△ABF≌△DAE；
（2）在（1）中，线段EF与AF、BF的等量关系是
（3）如图2，点G是CD边上任意一点（不与C、D两点重合），连接AG，作BF⊥AG于点F，DE⊥AG于点E．那么图中全等三角形是
可，不需要证明）．
查看习题详情和答案>>
正方形ABCD边长为4，M、N分别是BC、CD上的两个动点，当M点在BC上运动时，保持AM⊥MN，设MB=x
（1）证明：△ABM∽△MCN；
（2）若四边形ABCN的面积等于9，求x的值；
（3）当M点运动到什么位置时，以A、B、M为顶点的三角形和以A、M、N为顶点的三角形相似． 查看习题详情和答案>>
（1）证明：△ABM∽△MCN；
（2）若四边形ABCN的面积等于9，求x的值；
（3）当M点运动到什么位置时，以A、B、M为顶点的三角形和以A、M、N为顶点的三角形相似． 查看习题详情和答案>>
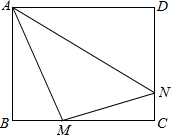正方形ABCD边长为4，M、N分别是BC、CD上的两个动点，当M点在BC上运动时，保持AM和MN垂直．（1）证明：Rt△ABM∽Rt△MCN；
（2）设BM=x，梯形ABCN的面积为y，求y与x之间的函数关系式；当M点运动到什么位置时，四边形ABCN面积最大，并求出最大面积．
四边形ABCD是正方形（正方形四边相等，四个角都是90°），BF⊥AG于点F，DE⊥AG于点E，
（1）如图1，若点G在BC边上时（不与点B、C重合），求证：△ABF≌△DAE；
（2）直接写出（1）中，线段EF与AF、BF的等量关系是
（3）①如图2，若点G在CD边上时（不与点C、D重合），则图中全等三角形是
②如图3，若点G在CD延长线上时，线段EF与AF、BF的等量关系是
（4）请画图、探究点G在BC延长线上时，线段EF与AF、BF的等量关系是
查看习题详情和答案>>
（1）如图1，若点G在BC边上时（不与点B、C重合），求证：△ABF≌△DAE；
（2）直接写出（1）中，线段EF与AF、BF的等量关系是
EF=AF-BF
EF=AF-BF
；（3）①如图2，若点G在CD边上时（不与点C、D重合），则图中全等三角形是
△ABF≌△DAE
△ABF≌△DAE
，线段EF与AF、BF的等量关系是EF=BF-AF
EF=BF-AF
；②如图3，若点G在CD延长线上时，线段EF与AF、BF的等量关系是
EF=AF+BF
EF=AF+BF
；（4）请画图、探究点G在BC延长线上时，线段EF与AF、BF的等量关系是
EF=BF-AF
EF=BF-AF
；（直接写出结果，不必证明）．