网址:http://m.1010jiajiao.com/timu_id_727746[举报]
一、选择题
1.选C; 科学计数法应表示为 的形式,其中1≤
的形式,其中1≤ <10.
<10.
2.选A; 在 中,电压U(V)一定时,电流I(A)关于电阻R(
中,电压U(V)一定时,电流I(A)关于电阻R( )的函数关系为反比例函数,图像为双曲线,但I、R均不能为负.
)的函数关系为反比例函数,图像为双曲线,但I、R均不能为负.
3.选B; 鞋店的经理关注众数,因为众数影响他的进货决定.
4.选A; 平行四边形的对边相等,所以周长等于邻边之和的2倍;因为BO=DO,所以△AOD的周长与△AOB的周长之差就是AD与AB的差.
5.选A; 用同一种图形可以平面镶嵌的是正三、四、六边形.
6.选A; 口袋中球的总数为4÷ 12.
12.
7.选D; 利用轴对称思想进行图形还原即可.
8.选D; 两条等式相减就得到 的不等式.
的不等式.
二、填空题
9. 10.
10. 11.
11.
16.3≤b≤6
三、解答题
19.解:原式=1+3-2× =4-1=3.
=4-1=3.
20.解:原式=
∵ ,
, ∴原式=
∴原式=
21.解:两边都除以2,得 . 移项得
. 移项得 .
.
配方得 ,
, .∴
.∴ 或
或 .
.
∴ .
.
22.解:(1)解方程 得
得 列表:
列表:
2
3
4
1
1,2
1,3
1,4
2
2,2
2,3
2,4
3
3,2
3,3
3,4
(或用树状图)
由表知:指针所指两数都是该方程解的概率是: ;指针所指两数都不是该方程解的概率是:
;指针所指两数都不是该方程解的概率是:
(2)不公平!∵1× ≠3×
≠3×
修改得分规则为:指针所指两个数字都是该方程解时,王磊得1分;指针所指两个数字都不是该方程解时,张浩得4分.此时1× =4×
=4×
23.(1)25% 5% (2)见图(补全每个图给2分)

(3)2000~2500(元/m2) (4)2500
24.(1)正方形、长方形、直角梯形.(任选两个均可)(填正确一个得1分)
(2)答案如图所示.M(3,4)或M(4,3).(没有写出不扣分)(根据图形给分,一个图形正确得l分)

(3)证明:连接EC,∵△ABC≌△DBE,∴.AC=DE,BC=BE.∵∠CBE=60°
∴EC=BC.∠BCE=60° ∵∠DCB=30° ∴∠DCE=90° ∴DC2+EC2=DE2
∴DC2+BC2=AC2.即四边形ABCD
25.解法(1):由题意转化为图a,设道路宽为 m(没画出图形不扣分)
m(没画出图形不扣分)

根据题意,可列出方程为
整理得
解得 50(舍去),
50(舍去), 2
2
答:道路宽为
解法(2):由题意转化为图b,设道路宽为 m,根据题意列方程得:
m,根据题意列方程得:


整理得:
解得: (舍去)
(舍去)
答:道路宽为
26.解法(1):∵OD⊥AB,∠A=30°
∴OA=OD÷tan30°=20 ,AD=2OD=40.
,AD=2OD=40.
∵AB是⊙O的直径,∴AB=40 ,且∠ACB=90°
,且∠ACB=90°
∴AC=AB?cos30°-40 ×
× 60
60
∴DC=AC-AD=60-40=20(cm)
解法(2):过点O作OE⊥AC于点E,如图
∵OD⊥AB于点O,∠A=30°,
∴AD=2OD=40,AO=OD÷tan30°=20
∴AE=AO?cos30°-20 ×
× 30
30
∵OE⊥AC于点E ∴AC=2AE=60.∴DC=AC-AD=60-40=20(cm)
解法(3):∵OD⊥AB于点O,AO=BO,∴AD=BD.∴∠1=∠A=30°
又∵AB为⊙O直径,∴∠ABC=60°.∴∠2=60°-30°=30°=∠A
又∵∠AOD=∠C=90°.∴△AOD≌△BCD ∴DC=OD=20(cm)

27.解:(1) .
.
∴ 与
与 的函数关系式为
的函数关系式为 .
.
(2) .
.
∴ 与
与 的函数关系式为
的函数关系式为 .
.
(3)令 480,得
480,得 ,
,
整理得 ,解得
,解得 .
.
将二次函数解析式变形为 画出大致图像如图.
画出大致图像如图.
由图像可知,要使月销售利润不低于480万元,产品的销售单价应在30元到38元之间(即30≤ ≤38).
≤38).

说明:解答题各小题只给了一种解答及评分说明,其他解法只要步骤合理、解答正确,均应给出相应分数.
28.解:(1)由题意知点C’的坐标为(3,-4).
设 的函数关系式为
的函数关系式为 .
.
又∵点A(1,0)在抛物线 上,∴
上,∴ ,解得
,解得 1.
1.
∴抛物线 的函数关系式为
的函数关系式为 (或
(或 ).
).
(2)∵P与P’始终关于 轴对称,∴PP’与
轴对称,∴PP’与 轴平行.
轴平行.
设点P的横坐标为m,则其纵坐标为 ,∵OD=4,
,∵OD=4,
∴ ,即
,即 .
.
当 时,解得
时,解得 .
.
当 时,解得
时,解得 .
.
∴当点P运动到( ,2)或(
,2)或( ,2)或(
,2)或( ,-2)或(
,-2)或( ,-2)时,
,-2)时,
P’P OD,以点D,O,P,P’为顶点的四边形是平行四边形.
OD,以点D,O,P,P’为顶点的四边形是平行四边形.
(3)满足条件的点M不存在.理由如下:若存在满足条件的点M在 上,
上,
则∠AMB=90°,∵∠RAM=30°(或∠ABM=30°),∴BM= AB=
AB= ×4=2.
×4=2.
过点M作MF⊥AB于点F,可得∠BMF=∠BAM=30°.
∴FB= BM=
BM= ×2=1,FM=
×2=1,FM= ,OF=4.
,OF=4.
∴点M的坐标为(4, ).
).
但是,当 4时,
4时, .
.
∴不存在这样的点M构成满足条件的直角三角形。
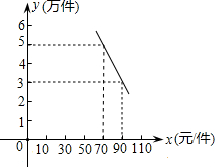 出每月销售量y(万件)与销售单价x(元/件)存在如图所示的一次函数关系.
出每月销售量y(万件)与销售单价x(元/件)存在如图所示的一次函数关系.(1)求y与x之间的函数关系式(不要求写出自变量x的取值范围);
(2)若公司计划12月份销售该产品获利70万元,并且要让客户尽量得到优惠,求销售单价x的值. 查看习题详情和答案>>
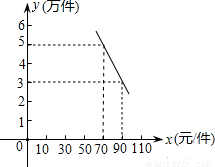
某环保器材公司销售一种新型产品,已知每件产品的进价为40元,经销过程中测 出每月销售量y(万件)与销售单价x(元/件)存在如图所示的一次函数关系.
出每月销售量y(万件)与销售单价x(元/件)存在如图所示的一次函数关系.
(1)求y与x之间的函数关系式(不要求写出自变量x的取值范围);
(2)若公司计划12月份销售该产品获利70万元,并且要让客户尽量得到优惠,求销售单价x的值.
查看习题详情和答案>>
(1)求y与x之间的函数关系式(不要求写出自变量x的取值范围);
(2)若公司计划12月份销售该产品获利70万元,并且要让客户尽量得到优惠,求销售单价x的值.
 查看习题详情和答案>>
查看习题详情和答案>>
一家用电器开发公司研制出一种新型电子产品,每件的生产成本为![]() 元,按定价
元,按定价![]() 元出售,每月可销售
元出售,每月可销售![]() 万件.为了增加销量,公司决定采取降价的办法,经市场调研,每降价
万件.为了增加销量,公司决定采取降价的办法,经市场调研,每降价![]() 元,月销售量可增加
元,月销售量可增加![]() 万件.
万件.
(1
)求出月销售量(2
)求出月销售利润(3
)请你通过(2)中的函数关系式及其大致图象帮助公司确定产品的销售单价范围,使月销售利润不低于查看习题详情和答案>>
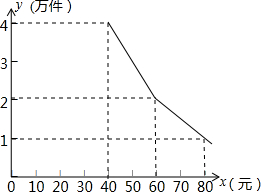 y(万件)与销售单价x(元)之间的函数关系如图所示
y(万件)与销售单价x(元)之间的函数关系如图所示(1)当40≤x≤60时,求月销售量y(万件)与销售单价x(元)之间的函数关系式;
(2)当销售单价定为50元时,为保证公司月利润达到5万元(利润=销售额-生产成本-员工工资-其它费用),该公司可安排员工多少人?
(3)若该公司有80名员工,求出公司利润W(万元)与x(元)之间的函数关系式;并说明该公司最早可在几个月后还清无息贷款? 查看习题详情和答案>>