摘要:当 --而点与,(,)与(,),--,都关于轴对称.这就是说.如果()在函数的图像上.那么.它关于轴对称的点(-)也在函数的图像上.这时.我们说函数关于轴对称.
网址:http://m.1010jiajiao.com/timu_id_725815[举报]
阅读下列材料再回答问题:
对于函数y=x2,当x=1时,y=1,当x=-1时,y=1;当x=2时,y=4,当x=-2时,y=4;…
而点(1,1)与(-1,1),(2,4)与(-2,4),…,都关于y轴对称.显然,如果点(x0,y0)在函数y=x2的图象上,那么,它关于y轴对称的点(-x0,y0)也在函数y=x2的图象上,这时,我们说函数y=x2关于y轴对称.
一般地,如果对于一个函数,当自变量x在允许范围内取值时,若x=x0和x=-x0时,函数值都相等,我们说函数的图象关于y轴对称.
问题:
(1)对于函数y=x3,当自变量x取一对相反数时,函数值也得到一对相反数,则函数y=x3的图象关于
(2)下列函数:①y=x3+2x;②y=2x4+4x2;③y=x+
;④y=-x-2 中,其图象关于y轴对称的有
(3)请你写出一个我们学过的函数关系式
查看习题详情和答案>>
对于函数y=x2,当x=1时,y=1,当x=-1时,y=1;当x=2时,y=4,当x=-2时,y=4;…
而点(1,1)与(-1,1),(2,4)与(-2,4),…,都关于y轴对称.显然,如果点(x0,y0)在函数y=x2的图象上,那么,它关于y轴对称的点(-x0,y0)也在函数y=x2的图象上,这时,我们说函数y=x2关于y轴对称.
一般地,如果对于一个函数,当自变量x在允许范围内取值时,若x=x0和x=-x0时,函数值都相等,我们说函数的图象关于y轴对称.
问题:
(1)对于函数y=x3,当自变量x取一对相反数时,函数值也得到一对相反数,则函数y=x3的图象关于
原点
原点
对称.(“x轴”、“y轴”或“原点”).(2)下列函数:①y=x3+2x;②y=2x4+4x2;③y=x+
| 1 |
| x |
②④
②④
,关于原点对称的有①③
①③
(只填序号).(3)请你写出一个我们学过的函数关系式
y=
(k≠0)
| k |
| x |
y=
(k≠0)
,其图象关于直线y=x对称.| k |
| x |
 24、如图在同一直角坐标系中,抛物线与两坐标轴分别交A(-1,0)、B(3,0)和C(0,-3),一次函数的图象与抛物线交于B、C两点.
24、如图在同一直角坐标系中,抛物线与两坐标轴分别交A(-1,0)、B(3,0)和C(0,-3),一次函数的图象与抛物线交于B、C两点.(1)抛物线解析式是
y=x2-2x-3
;(2)抛物线的顶点坐标是
(1,-4)
;对称轴是x=1
;(3)当自变量x满足
x>1
时,两函数值都随x的增大而增大;(4)当自变量x满足
0<x<3
时,一次函数值大于二次函数值.(5)此抛物线关于x轴对称的新抛物线解析式是
y=-x2+2x+3
.
如图,一次函数y1=x+1的图象与反比例函数y2=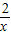 的图象交与A(1,M),B(n,-1)两点,过点A作AC⊥x轴于点C,过点B作BD⊥x轴于点D,连接AO,BO.得出以下结论:
的图象交与A(1,M),B(n,-1)两点,过点A作AC⊥x轴于点C,过点B作BD⊥x轴于点D,连接AO,BO.得出以下结论:
①点A和点B关于直线y=-x对称;
②当x<1时,y2>y1;
③S△AOC=S△BOD;
④当x>0时,y1,y2都随x的增大而增大.
其中正确的是( )

A.①②③
B.②③
C.①③
D.①②③④
查看习题详情和答案>>
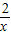 的图象交与A(1,M),B(n,-1)两点,过点A作AC⊥x轴于点C,过点B作BD⊥x轴于点D,连接AO,BO.得出以下结论:
的图象交与A(1,M),B(n,-1)两点,过点A作AC⊥x轴于点C,过点B作BD⊥x轴于点D,连接AO,BO.得出以下结论:①点A和点B关于直线y=-x对称;
②当x<1时,y2>y1;
③S△AOC=S△BOD;
④当x>0时,y1,y2都随x的增大而增大.
其中正确的是( )

A.①②③
B.②③
C.①③
D.①②③④
查看习题详情和答案>>
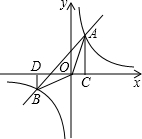 如图,一次函数y1=x+1的图象与反比例函数y2=
如图,一次函数y1=x+1的图象与反比例函数y2= 的图象交与A(1,M),B(n,-1)两点,过点A作AC⊥x轴于点C,过点B作BD⊥x轴于点D,连接AO,BO.得出以下结论:
的图象交与A(1,M),B(n,-1)两点,过点A作AC⊥x轴于点C,过点B作BD⊥x轴于点D,连接AO,BO.得出以下结论: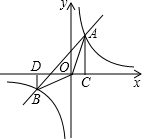 (2013•保定二模)如图,一次函数y1=x+1的图象与反比例函数y2=
(2013•保定二模)如图,一次函数y1=x+1的图象与反比例函数y2=