网址:http://m.1010jiajiao.com/timu_id_70771[举报]
1-15 D AC AC A ABAA BC
13. 14.40 15.
14.40 15. 或
或
16. 
17.证明:(Ⅰ)



 函数
函数 在
在 上为增函数;
上为增函数;
(Ⅱ)反证法:假设存在 ,满足
,满足
则
这与 矛盾,假设错误
矛盾,假设错误
故方程 没有负数根
没有负数根
18.解:依题意有: = a,
= a,
 =2ax+
=2ax+ (x<2)
(x<2)
 方程为
方程为 =0
=0
 与圆相切
与圆相切 
 =
=
 a=
a=
19.解:(Ⅰ) ,
……………………………2分
,
……………………………2分
∴ ,
……………………………3分
,
……………………………3分
又 ,
……………………………4分
,
……………………………4分
∴曲线 在
在 处的切线方程为
处的切线方程为 , …………5分
, …………5分
即 .
…………………6分
.
…………………6分
(Ⅱ)由 消去
消去 得
得 ,解得
,解得 ,
, ,……7分
,……7分
所求面积 , …………9分
, …………9分
设 ,则
,则 , …………10分
, …………10分
∴
 .
……………………12分
.
……………………12分

21.(1)当 时
时 ,当
,当 时,
时, .
.
由条件可知, ,即
,即 解得
解得
∵  ………….5分
………….5分
(2)当 时,
时,
即





故m的取值范围是 …………….12分
…………….12分
22. 解:(I)因为 ,所以
,所以 ----1分
----1分
 ,
,
解得 ,
------------------------3分
,
------------------------3分
此时 ,
,
当 时
时 ,当
,当 时
时 ,
----------5分
,
----------5分
所以 时
时 取极小值,所以
取极小值,所以 符合题目条件;
----------6分
符合题目条件;
----------6分
(II)由 得
得 ,
,
当 时,
时, ,此时
,此时 ,
, ,
,
 ,所以
,所以 是直线
是直线 与曲线
与曲线 的一个切点;
-----8分
的一个切点;
-----8分
当 时,
时, ,此时
,此时 ,
, ,
,
 ,所以
,所以 是直线
是直线 与曲线
与曲线 的一个切点;
-----------10分
的一个切点;
-----------10分
所以直线l与曲线S相切且至少有两个切点;
对任意x∈R, ,
,
所以
因此直线 是曲线
是曲线 的“上夹线”. ---------------------14分
的“上夹线”. ---------------------14分
22.【解】(Ⅰ)
∴ 的增区间为
的增区间为 ,
, 减区间为
减区间为 和
和 .
.
极大值为 ,极小值为
,极小值为 .…………4′
.…………4′
(Ⅱ)原不等式可化为 由(Ⅰ)知,
由(Ⅰ)知, 时,
时, 的最大值为
的最大值为 .
.
∴ 的最大值为
的最大值为 ,由恒成立的意义知道
,由恒成立的意义知道 ,从而
,从而 …8′
…8′
(Ⅲ)设
则 .
.
∴当 时,
时, ,故
,故 在
在 上是减函数,
上是减函数,
又当 、
、 、
、 、
、 是正实数时,
是正实数时,
∴ .
.
由 的单调性有:
的单调性有: ,
,
即 .…………12′
.…………12′
已知函数f(x)=![]() ,g(x)=alnx,a
,g(x)=alnx,a![]() R。
R。
(1) 若曲线y=f(x)与曲线y=g(x)相交,且在交点处有相同的切线,求a的值及该切线的方程;
(2) 设函数h(x)=f(x)- g(x),当h(x)存在最小之时,求其最小值![]() (a)的解析式;
(a)的解析式;
对
(2)中的![]() (a),证明:当a
(a),证明:当a![]() (0,+
(0,+![]() )时,
)时, ![]() (a)
(a)![]() 1.
1.
(本小题满分14分)
已知函数f(x)=![]() ,g(x)=alnx,a
,g(x)=alnx,a![]() R。
R。
若曲线y=f(x)与曲线y=g(x)相交,且在交点处有相同的切线,求a的值及该切线的方程;
设函数h(x)=f(x)- g(x),当h(x)存在最小之时,求其最小值![]() (a)的解析式;
(a)的解析式;
对(2)中的![]() (a),证明:当a
(a),证明:当a![]() (0,+
(0,+![]() )时,
)时, ![]() (a)
(a)![]() 1.
1.
(本小题满分14分)
已知函数f(x)=![]() ,g(x)=alnx,a
,g(x)=alnx,a![]() R。
R。
若曲线y=f(x)与曲线y=g(x)相交,且在交点处有相同的切线,求a的值及该切线的方程;
设函数h(x)=f(x)- g(x),当h(x)存在最小之时,求其最小值![]() (a)的解析式;
(a)的解析式;
对(2)中的![]() (a),证明:当a
(a),证明:当a![]() (0,+
(0,+![]() )时,
)时, ![]() (a)
(a)![]() 1.
1.
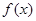 =
=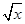 ,
,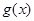 =alnx,a
=alnx,a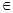 R。
R。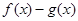 ,当h(x)存在最小之时,求其最小值
,当h(x)存在最小之时,求其最小值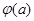 的解析式;
的解析式; )时,
)时, 1.
1.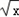 ,g(x)=alnx,a
,g(x)=alnx,a R.
R. 的解析式;
的解析式;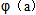 ,证明:当a
,证明:当a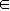 (0,+
(0,+ )时,
)时,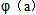
 1
1