摘要：在下面( )里填上“＞ “＜或“= .

网址：http://m.1010jiajiao.com/timu_id_695302[举报]

请在下面“□”、“○”中分别填上适当的代数式，是等式□+○=

查看习题详情和答案>>

请在下面“□”、“○”中分别填上适当的代数式，是等式□+○= $数学公式$ 成立．

查看习题详情和答案>>

请在下面“□”、“○”中分别填上适当的代数式，是等式□+○=

查看习题详情和答案>>

完成下面的证明推理过程，并在括号里填上根据．如图，已知∠1= ∠2 ，∠A= ∠F ，
求证：∠C= ∠D.

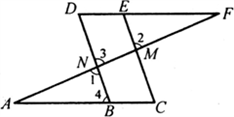
证明：因为∠1=∠2（已知），∠1=∠3（对顶角相等）
所以∠2=∠____(    )
所以BD∥____(    )
所以∠FEM=∠D，∠4=∠C(    )
又因为∠A=∠F(已知)
所以AC∥DF(    )
所以∠C=∠FEM(    )
又因为∠FEM=∠D(已证)
所以∠C=∠D(等量代换)

查看习题详情和答案>>

阅读下面的材料，并完成填空，
你能比较两个数2013²⁰¹⁴与2014²⁰¹³的大小吗？为了解决这个问题，先问题一般化，
即比较nⁿ⁺¹和（n+1）ⁿ的大小（n≥1的整数）然后从分析n=1、2、3、4、5…这些简单情况入手，从中发现规律，经过归纳猜想出结论．
（1）通过计算比较下列各组两个数的大小（在横线上填上“＞”“＜”或“=”）
①1²

5⁴； ⑤5⁶

6⁵
（2）根据第（1）小题结果经过归纳，可以猜想出nⁿ⁺¹和（n+1）ⁿ怎样的大小关系？
（3）根据上面的归纳猜想得到的一般结论，判断2013²⁰¹⁴与2014²⁰¹³的大小关系．

查看习题详情和答案>>