摘要:24.下表是某市移动通信公司刚刚推出的两种本地通讯业务.请根据表中的两种计费方式.回答下列问题: (1)对于某个本地通话时间.会出现按两种计费方式收费一样多吗? (2)若张华估计每月的本地通话时间约是300分钟.你认为他采用哪种计费方式较合算? 方式一方式二月租费018元/月本地通话费
网址:http://m.1010jiajiao.com/timu_id_694572[举报]
【改编】(本小题满分10分)
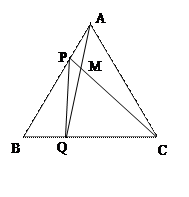
数形结合作为一种数学思想方法,数形结合的应用大致又可分为两种情形:或者借助于数的精确性来阐明形的某些属性,即“以数解形”;或者借助形的 几何直观性来阐明数之间的某种关系,即“以形助数”。 如浙教版九上课本第109页作业题第2题:如图1,已知在△ABC中,∠ACB=900,CD⊥AB,D为垂足。易证得两个结论:(1)AC·BC = AB·CD (2)AC2= AD·AB
几何直观性来阐明数之间的某种关系,即“以形助数”。 如浙教版九上课本第109页作业题第2题:如图1,已知在△ABC中,∠ACB=900,CD⊥AB,D为垂足。易证得两个结论:(1)AC·BC = AB·CD (2)AC2= AD·AB
(1)请你用数形结合的“以数解形”思想来解:如图2,已知在△ABC中(AC>BC),∠ACB=900,CD⊥AB,D为垂足, CM平分∠ACB,且BC、AC是方程x2-14x+48=0的两个根,求AD、MD的长。
(2)请你用数形结合的“以形助数”思想来解:设a、b、c、d都是正数,满足a:b=c:d,且a最大。求证:a+d>b+c(提示:不访设AB=a,CD=d,AC=b,BC=c,构造图1)

(本小题满分10分)
如图,AB = 3AC,BD = 3AE,又BD∥AC,点B,A,E在同一条直线上. 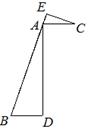
(1) 求证:△ABD∽△CAE;
(2) 如果AC =BD,AD =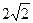 BD,设BD = a,求BC的长.
BD,设BD = a,求BC的长.
(本小题满分10分)李华在学校组织的社会调查活动中负责了解他所居住的小区600户居民的家庭收入情况.他从中随机调查了40户居民家庭收入情况(收入取整数,单位:元),并绘制了如下的频数分布表和频数分布直方图.
| 分组 | 频数 | 百分比 |
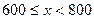 | 2 | 5% |
800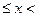 1000 1000 | 6 | 15% |
1000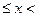 12000 12000 | | 45% |
| | 9 | 22.5% |
| | | |
1600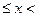 1800 1800 | 2 | |
| 合计 | 40 | 100% |

根据以上提供的信息,解答下列问题:
(1)补全频数分布表.
(2)补全频数分布直方图.
(3)请你估计该居民小区家庭属于中等收入(大于1000不足1600元)的大约有多少户? 查看习题详情和答案>>