摘要:如图所示 .AC交BD于点O.请你从下面三项中选出两个作为条件.另一个作为结论写出一个真命题.并加以证明.(1)OA=OC (2)OB=OD (3)AB∥CD
网址:http://m.1010jiajiao.com/timu_id_690717[举报]
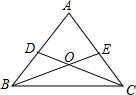 在一次数学课上,周老师在屏幕上出示了一个例题:
在一次数学课上,周老师在屏幕上出示了一个例题:在△ABC中,D,E分别是AB,AC上的一点,BE与CD交于点O,画出图形(如图),
给出下列四个条件:①∠DBO=∠ECO;②∠BDO=∠CEO;③BD=CE;④OB=OC.
(1)要求同学从这四个等式中选出两个作为已知条件,可判定△ABC是等腰三角形.
请你用序号在横线上写出所有情形.答:
①③,①④,②③和②④
①③,①④,②③和②④
;(4分)(2)选择第(1)题中的一种情形,说明是△ABC等腰三角形的理由,并写出解题过程.解:我选择
①④
①④
.(6分) 在一次数学课上,周老师在屏幕上出示了一个例题:
在一次数学课上,周老师在屏幕上出示了一个例题:
在△ABC中,D,E分别是AB,AC上的一点,BE与CD交于点O,画出图形(如图),
给出下列四个条件:①∠DBO=∠ECO;②∠BDO=∠CEO;③BD=CE;④OB=OC.
(1)要求同学从这四个等式中选出两个作为已知条件,可判定△ABC是等腰三角形.
请你用序号在横线上写出所有情形.答:______;
(2)选择第(1)题中的一种情形,说明是△ABC等腰三角形的理由,并写出解题过程.解:我选择______.
查看习题详情和答案>>
在一次数学课上,周老师在屏幕上出示了一个例题:
在△ABC中,D,E分别是AB,AC上的一点,BE与CD交于点O,画出图形(如图),
给出下列四个条件:①∠DBO=∠ECO;②∠BDO=∠CEO;③BD=CE;④OB=OC.
(1)要求同学从这四个等式中选出两个作为已知条件,可判定△ABC是等腰三角形.
请你用序号在横线上写出所有情形.答:______;(4分)
(2)选择第(1)题中的一种情形,说明是△ABC等腰三角形的理由,并写出解题过程.解:我选择______.(6分)
 查看习题详情和答案>>
查看习题详情和答案>>
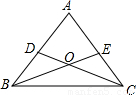
在△ABC中,D,E分别是AB,AC上的一点,BE与CD交于点O,画出图形(如图),
给出下列四个条件:①∠DBO=∠ECO;②∠BDO=∠CEO;③BD=CE;④OB=OC.
(1)要求同学从这四个等式中选出两个作为已知条件,可判定△ABC是等腰三角形.
请你用序号在横线上写出所有情形.答:______;(4分)
(2)选择第(1)题中的一种情形,说明是△ABC等腰三角形的理由,并写出解题过程.解:我选择______.(6分)
 查看习题详情和答案>>
查看习题详情和答案>>
如图所示,在正方形ABCD中,对角线AC与BD相交于点E, AF平分∠BAC,交BD于点F.

(1)求证:![]()
(2)点![]() 从点C出发,沿着线段CB向点B运动(不与点B重合),同时点
从点C出发,沿着线段CB向点B运动(不与点B重合),同时点![]() 从点A出发,沿着BA的延长线运动,点
从点A出发,沿着BA的延长线运动,点![]() 与
与![]() 的运动速度相同,当动点
的运动速度相同,当动点![]() 停止运动时,另一动点
停止运动时,另一动点![]() 也随之停止运动.如图所示,
也随之停止运动.如图所示,![]() 平分
平分![]() ,交BD于点
,交BD于点![]() ,过点
,过点![]() 作
作![]() 垂足为
垂足为![]() ,请猜想
,请猜想![]() 与AB三者之间的数量关系,并证明你的猜想;
与AB三者之间的数量关系,并证明你的猜想;

(3) 在(2)的条件下,当![]() 时,求BD的长.
时,求BD的长.
数学活动课上,甲、乙两位同学在研究一道数学题:“已知:如图1,在△ABC和△DEF中,∠A=∠D=90°,∠B=50°,∠E=32°,且BC=EF.试画直线m,l,使直线m将△ABC分成的两个小三角形与直线l将△DEF分成的两个小三角形分别相似,并标出每个小三角形各内角的度数.”
甲同学是这样做的:如图2,使得两个直角三角形的斜边重合,以斜边中点0为圆心,OB长为半径作出辅助圆,根据到定点的距离等于定长的点在圆上,可知A、B(E)、C(F)、D在⊙0上.设BD所在的直线m与AC所在的直线l交于点G,根据同弧所对的圆周角相等,由∠ABC=50°,∠DEF=32°,易求得∠ABG=DFG=18°,再由∠A=∠D=90°,可求得∠AGB=∠DGF=72°,∠GCB=40°,∠BGC=108°,从而△AGB∽△DGF.△GBC∽△GEF.
乙同学在甲同学的启发下,利用辅助圆又补充了其它分割方法.
你看明白甲同学的分割方法了吗?请你仿照甲同学的方法,把这道题其它的所有分割方法补充完整.
要求:不需写解答过程.如图2所示.利用辅助圆画出示意图,标明直线及每个小三角形各内角的度数即可.
查看习题详情和答案>>
甲同学是这样做的:如图2,使得两个直角三角形的斜边重合,以斜边中点0为圆心,OB长为半径作出辅助圆,根据到定点的距离等于定长的点在圆上,可知A、B(E)、C(F)、D在⊙0上.设BD所在的直线m与AC所在的直线l交于点G,根据同弧所对的圆周角相等,由∠ABC=50°,∠DEF=32°,易求得∠ABG=DFG=18°,再由∠A=∠D=90°,可求得∠AGB=∠DGF=72°,∠GCB=40°,∠BGC=108°,从而△AGB∽△DGF.△GBC∽△GEF.
乙同学在甲同学的启发下,利用辅助圆又补充了其它分割方法.
你看明白甲同学的分割方法了吗?请你仿照甲同学的方法,把这道题其它的所有分割方法补充完整.

要求:不需写解答过程.如图2所示.利用辅助圆画出示意图,标明直线及每个小三角形各内角的度数即可.