题目内容
 在一次数学课上,周老师在屏幕上出示了一个例题:
在一次数学课上,周老师在屏幕上出示了一个例题:
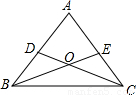
在△ABC中,D,E分别是AB,AC上的一点,BE与CD交于点O,画出图形(如图),
给出下列四个条件:①∠DBO=∠ECO;②∠BDO=∠CEO;③BD=CE;④OB=OC.
(1)要求同学从这四个等式中选出两个作为已知条件,可判定△ABC是等腰三角形.
请你用序号在横线上写出所有情形.答:______;
(2)选择第(1)题中的一种情形,说明是△ABC等腰三角形的理由,并写出解题过程.解:我选择______.
解:(1)①③,①④,②③和②④;
(2)以①④为条件,理由:
∵OB=OC,
∴∠OBC=∠OCB.
又∵∠DBO=∠ECO,
∴∠DBO+∠OBC=∠ECO+∠OCB,即∠ABC=∠ACB,
∴AB=AC,
∴△ABC是等腰三角形.
故答案为:①③,①④,②③和②④;①④.
分析:(1)要证△ABC是等腰三角形,就要证∠ABC=∠ACB,根据已知条件即可找到证明∠ABC=∠ACB的组合;
(2)可利用△DOB与△EOC全等,得出OC=OB,再得出∠OCB与∠OBC相等,就能证明∠ABC与∠ACB相等.
点评:此题主要考查利用等角对等边来判定等腰三角形;题目对学生的要求比较高,利用等量加等量和相等是正确解答本题的关键.
(2)以①④为条件,理由:
∵OB=OC,
∴∠OBC=∠OCB.
又∵∠DBO=∠ECO,
∴∠DBO+∠OBC=∠ECO+∠OCB,即∠ABC=∠ACB,
∴AB=AC,
∴△ABC是等腰三角形.
故答案为:①③,①④,②③和②④;①④.
分析:(1)要证△ABC是等腰三角形,就要证∠ABC=∠ACB,根据已知条件即可找到证明∠ABC=∠ACB的组合;
(2)可利用△DOB与△EOC全等,得出OC=OB,再得出∠OCB与∠OBC相等,就能证明∠ABC与∠ACB相等.
点评:此题主要考查利用等角对等边来判定等腰三角形;题目对学生的要求比较高,利用等量加等量和相等是正确解答本题的关键.

练习册系列答案
相关题目

 在一次数学课上,周老师在屏幕上出示了一个例题:
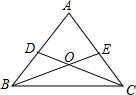
在一次数学课上,周老师在屏幕上出示了一个例题: 在一次数学课上,陈老师在黑板上画出下图,并写下了四个等式:
在一次数学课上,陈老师在黑板上画出下图,并写下了四个等式: