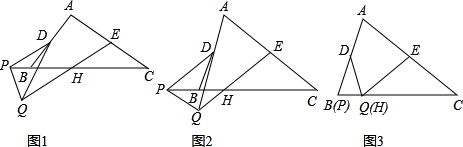
摘要:23.如图13.在△AFD和△CEB中.点A.E.F.C在同一直线上.有下面四个论断:∠B=∠D.(4)AD//BC.请用其中三个作为条件.余下一个作为结论.编一道数学问题.并写出解答过程.
网址:http://m.1010jiajiao.com/timu_id_690621[举报]
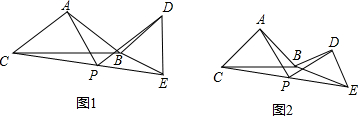
(2007•临夏州)[(1)-(3),10分]如图,已知等边△ABC和点P,设点P到△ABC三边AB、AC、BC(或其延长线)的距离分别为h1、h2、h3,△ABC的高为h.
在图(1)中,点P是边BC的中点,此时h3=0,可得结论:h1+h2+h3=h.
在图(2)--(5)中,点P分别在线段MC上、MC延长线上、△ABC内、△ABC外.
(1)请探究:图(2)--(5)中,h1、h2、h3、h之间的关系;(直接写出结论)
(2)证明图(2)所得结论;
(3)证明图(4)所得结论.
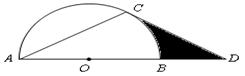
(4)在图(6)中,若四边形RBCS是等腰梯形,∠B=∠C=60°,RS=n,BC=m,点P在梯形内,且点P到四边BR、RS、SC、CB的距离分别是h1、h2、h3、h4,桥形的高为h,则h1、h2、h3、h4、h之间的关系为:

查看习题详情和答案>>
在图(1)中,点P是边BC的中点,此时h3=0,可得结论:h1+h2+h3=h.
在图(2)--(5)中,点P分别在线段MC上、MC延长线上、△ABC内、△ABC外.
(1)请探究:图(2)--(5)中,h1、h2、h3、h之间的关系;(直接写出结论)
(2)证明图(2)所得结论;
(3)证明图(4)所得结论.
(4)在图(6)中,若四边形RBCS是等腰梯形,∠B=∠C=60°,RS=n,BC=m,点P在梯形内,且点P到四边BR、RS、SC、CB的距离分别是h1、h2、h3、h4,桥形的高为h,则h1、h2、h3、h4、h之间的关系为:
m(h1+h2+h3)-n(h1+h3-h4)=(m+n)h
m(h1+h2+h3)-n(h1+h3-h4)=(m+n)h
;图(4)与图(6)中的等式有何关系?
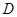 在
在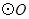 的直径
的直径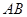 的延长线上,点
的延长线上,点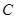 在
在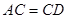 ,
,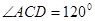 ,
,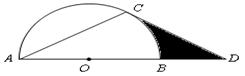
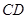 是
是