题目内容
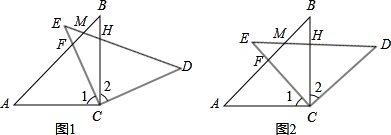
如图1，在△ABC和△DBE中，AB=AC，DB=DE，∠CAB+∠BDE=180°，∠CAB=α，P为CE的中点，连接AP、DP．若α=120°，探究线段AP、DP的关系．
说明：如果你经过反复探索没有解决问题，可以更改条件将“α=120°”改为“α=90°”，选取图2完成证明得10分．
说明：如果你经过反复探索没有解决问题，可以更改条件将“α=120°”改为“α=90°”，选取图2完成证明得10分．
分析：根据等腰三角形的性质得出∠AGB=∠BHD，∠ABG=∠1，即可得出△AGB∽△BHD，进而得出四边形GPHB为平行四边形，再得出△DHP∽△PGA，得出线段AP、DP的关系．
解答：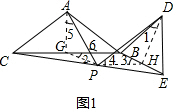
解：AP⊥DP，
AP=DP．
分别取BC、BE的中点G、H，连接AG、PG、DH、PH，
∵AB=AC，∴∠AGB=90°，
又∵α=120°，
∴∠GAB=
α=60°，∠ABG=30°，BG=
AG，
∵∠CAB+∠BDE=180°，∴∠BDE=60°，
同理可得∠DHB=90°，∠1=30°，
∴∠AGB=∠BHD，∠ABG=∠1，
∴△AGB∽△BHD，
∴
=
，
∵P为CE的中点，H为BE的中点，
∴PH∥BG，PH=
BC=BG，
∴四边形GPHB为平行四边形，
∴BH=PG，∠2=∠3，
∴
=
，即
=
，∠DHP=∠PGA，
∴△DHP∽△PGA，
∴∠4=∠5，
=
=
=
，
∠6=∠5+90°=∠4+∠APD，
∴∠APD=90°，
即AP⊥DP，
AP=DP．
解：AP⊥DP，| 3 |
分别取BC、BE的中点G、H，连接AG、PG、DH、PH，
∵AB=AC，∴∠AGB=90°，
又∵α=120°，
∴∠GAB=
| 1 |
| 2 |
| 3 |
∵∠CAB+∠BDE=180°，∴∠BDE=60°，
同理可得∠DHB=90°，∠1=30°，
∴∠AGB=∠BHD，∠ABG=∠1，
∴△AGB∽△BHD，
∴
| DH |
| BG |
| BH |
| AG |
∵P为CE的中点，H为BE的中点，
∴PH∥BG，PH=
| 1 |
| 2 |
∴四边形GPHB为平行四边形，
∴BH=PG，∠2=∠3，
∴
| DH |
| PH |
| PG |
| AG |
| DH |
| PG |
| PH |
| AG |
∴△DHP∽△PGA，
∴∠4=∠5，
| PD |
| PA |
| PH |
| AG |
| BG |
| AG |
| 3 |
∠6=∠5+90°=∠4+∠APD，
∴∠APD=90°，
即AP⊥DP，
| 3 |
点评：此题主要考查了等腰三角形的性质以及相似三角形的性质与判定和平行四边形的判定，熟练应用相似三角形的性质得出是解题关键．
练习册系列答案
灵星计算小达人系列答案
孟建平错题本系列答案
相关题目
