摘要：(2)当为何值时.的面积有最大值.最大值为多少?
网址：http://m.1010jiajiao.com/timu_id_686252[举报]
[提出问题]：已知矩形的面积为1，当该矩形的长为多少时，它的周长最小？最小值是多少？
[建立数学模型]：设该矩形的长为x，周长为y，则y与x的函数关系式为y=x+
（x＞0）．
[探索研究]：我们可以借鉴以前研究函数的经验，先探索函数y=x+（x＞0）的图象和性质．
①填写下表，画出函数的图象；
| x | … |  |  |  | 1 | 2 | 3 | 4 | … |
| y | … | … |
（x＞0）有最小值；③我们在课堂上求二次函数最大（小）值时，除了通过观察图象，还可以通过配方得到．请你通过配方求函数y=x+
（x＞0）的最小值．
查看习题详情和答案>>
[提出问题]：已知矩形的面积为1，当该矩形的长为多少时，它的周长最小？最小值是多少？
[建立数学模型]：设该矩形的长为x，周长为y，则y与x的函数关系式为y=x+
（x＞0）．
[探索研究]：我们可以借鉴以前研究函数的经验，先探索函数y=x+（x＞0）的图象和性质．
①填写下表，画出函数的图象；
②观察图象，写出当自变量x取何值时，函数y=x+
（x＞0）有最小值；
③我们在课堂上求二次函数最大（小）值时，除了通过观察图象，还可以通过配方得到．请你通过配方求函数y=x+
（x＞0）的最小值．
查看习题详情和答案>>
[建立数学模型]：设该矩形的长为x，周长为y，则y与x的函数关系式为y=x+
（x＞0）．[探索研究]：我们可以借鉴以前研究函数的经验，先探索函数y=x+（x＞0）的图象和性质．
①填写下表，画出函数的图象；
| x | … |  |  |  | 1 | 2 | 3 | 4 | … |
| y | … | … |
（x＞0）有最小值；③我们在课堂上求二次函数最大（小）值时，除了通过观察图象，还可以通过配方得到．请你通过配方求函数y=x+
（x＞0）的最小值．
查看习题详情和答案>>
如图，在直角坐标系中，梯形ABCD的底边AB在x轴上，底边CD的端点D在y轴上．直线CB的表达式为y=-
x+
，点A、D的坐标分别为（-4，0），（0，4）．动点P自A点出发，在AB上匀速运行．动点Q自点B出发，在折线BCD上匀速运行，速度均为每秒1个单位．当其中一个动点到达终点时，它们同时停止运动．设点P运动t（秒）时，△OPQ的面积为s（不能构成△OPQ的动点除外）．
（1）求出点B、C的坐标；
（2）求s随t变化的函数关系式；
（3）当t为何值时s有最大值？并求出最大值．
查看习题详情和答案>>
| 4 |
| 3 |
| 16 |
| 3 |
（1）求出点B、C的坐标；
（2）求s随t变化的函数关系式；
（3）当t为何值时s有最大值？并求出最大值．
查看习题详情和答案>>
已知，在直角坐标系中，△ABO的位置如图1，点O是坐标原点，点A的坐标为（-3，4），AB=AO，AB∥x轴交于y轴于点H．
（1）填空：点B的坐标（
（2）把△ABO沿直线OB翻折得到△CBO，连接AC交于y轴于点M，请在图2 中画出图形，并判断此时四边形AOCB的形状，说明理由．
（3）连接BM，动点P从点A出发，沿折线ABC方向向终点C匀速运动，点P的运动时间为t秒，点P的速度为每秒2个单位，设△PMB的面积为S（S≠0），求当t为何值时，S有最大值，并求出S的最大值．
（4）在（3）条件下，点P在运动过程中，当∠MPB+∠BCO=90°时，求直线OP与直线AC所夹锐角的正切值．
查看习题详情和答案>>
（1）填空：点B的坐标（
2
2
，4
4
），△ABO的面积是10
10
．（2）把△ABO沿直线OB翻折得到△CBO，连接AC交于y轴于点M，请在图2 中画出图形，并判断此时四边形AOCB的形状，说明理由．
（3）连接BM，动点P从点A出发，沿折线ABC方向向终点C匀速运动，点P的运动时间为t秒，点P的速度为每秒2个单位，设△PMB的面积为S（S≠0），求当t为何值时，S有最大值，并求出S的最大值．
（4）在（3）条件下，点P在运动过程中，当∠MPB+∠BCO=90°时，求直线OP与直线AC所夹锐角的正切值．
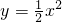，把它平移后得抛物线C2，使C2经过点A（0，8），且与抛物线C1交于点B（2，n）．在x轴上有一点P，从原点O出发以每秒1个单位的速度沿x轴正半轴的方向移动，设点P移动的时间为t秒，过点P作x轴的垂线l，分别交抛物线C1、C2于E、D，当直线l经过点B前停止运动，以DE为边在直线l左侧画正方形DEFG．