摘要:27.四边形一条对角线所在直线上的点.如果到这条对角线的两端点的距离不相等.但到另一对角线的两个端点的距离相等.则称这点为这个四边形的准等距点.如图l.点P为四边形ABCD对角线AC所在直线上的一点.PD=PB.PA≠PC.则点P为四边形ABCD的准等距点.
网址:http://m.1010jiajiao.com/timu_id_686027[举报]
已知四边形![]() 是矩形,
是矩形,![]() ,直线
,直线![]() 分别与
分别与![]() 交与
交与![]() 两点,
两点,![]() 为对角线
为对角线![]() 上一动点(
上一动点(![]() 不与
不与![]() 重合).
重合).
(1)当点![]() 分别为
分别为![]() 的中点时,(如图1)问点
的中点时,(如图1)问点![]() 在
在![]() 上运动时,点
上运动时,点![]() 、
、![]() 、
、![]() 能否构成直角三角形?若能,共有几个,并在图1中画出所有满足条件的三角形.
能否构成直角三角形?若能,共有几个,并在图1中画出所有满足条件的三角形.
(2)若![]() ,
,![]() ,
,![]() 为
为![]() 的中点,当直线
的中点,当直线![]() 移动时,始终保持
移动时,始终保持![]() ,(如图2)求
,(如图2)求![]() 的面积
的面积![]() 与
与![]() 的长
的长![]() 之间的函数关系式.
之间的函数关系式.

已知四边形
ABCD是矩形,BC>AB,直线MN分别与AB,BC交与E,F两点,P为对角线AC上一动点(P不与A,C重合).(1)
当点E,F分别为AB,BC的中点时,(如图)问点P在AC上运动时,点P,E,F能否构成直角三角形?若能,共有几个,请在图中画出所有满足条件的三角形.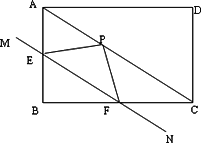
(2)
若AB=3,BC=4,P为AC的中点,当直线MN的移动时,始终保持MN∥AC,(如图)求△PEF的面积S△PEF与FC的长x之间的函数关系式.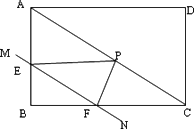
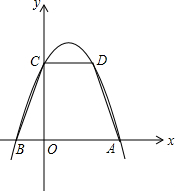 如图,在直角坐标系中,等腰梯形ABCD中,AB∥CD,AD=BC=
如图,在直角坐标系中,等腰梯形ABCD中,AB∥CD,AD=BC= ,AB=4,CD=2.抛物线y=ax2+bx+c经过A、B、C三点.
,AB=4,CD=2.抛物线y=ax2+bx+c经过A、B、C三点. ,AB=4,CD=2.抛物线y=ax2+bx+c经过A、B、C三点.
,AB=4,CD=2.抛物线y=ax2+bx+c经过A、B、C三点.
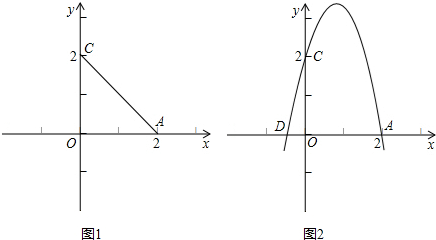
 ,0),过A,C,D的抛物线与(1)所得的四边形OABC的边BC交于点E,求抛物线的解析式及点E的坐标;
,0),过A,C,D的抛物线与(1)所得的四边形OABC的边BC交于点E,求抛物线的解析式及点E的坐标;