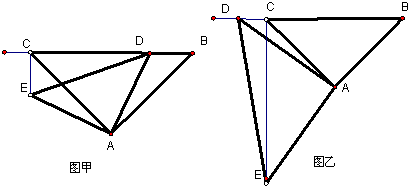
摘要：23．已知△ABC中.AB=AC.∠A为锐角.直线BC上有一点P.过点P分别作PD⊥AB于D.PE⊥AC于E.过点C作CF⊥AB于F． (1)你认为点P的位置有几种情形?请分别画出符合上述题意的图形．(2)在相应的图形下分别猜测并写出线段PD.PE.CF之间存在的等式关系． 中的一个关系式加以证明.(提示:本题可能用到的结论有:①有三个角是直角的四边形是长方形 ②长方形的对边相等)
网址：http://m.1010jiajiao.com/timu_id_685810[举报]
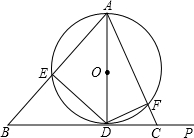
已知△ABC中，AB＝AC，以AB为直径的⊙O交BC于D，交AC于E．
(1)如图，若AB＝6，CD＝2，求CE的长．
(2)如图，当∠A为锐角时，连接BE，试判断∠BAC与∠CBE的关系，并证明你的结论．
(3)若上图中的边AB不动，边AC绕点A按逆时针旋转，当∠BAC为钝角时，如下图，CA的延长线与⊙O相交于E．
请问：∠BAC与∠CBE的关系是否与(2)中你得出的关系相同？若相同，请加以证明；若不同，请说明理由．
查看习题详情和答案>>已知△ABC中，AB＝AC，以AB为直径的⊙O交BC于D，交AC于E．
(1)如图①，若AB＝6，CD＝2，求：CE的长；
(2)如图②，当∠A为锐角时，连结BE，试判断∠BAC与∠CBE的关系，并证明你的结论；
(3)若图②中的边AB不动，边AC绕点A按逆时针旋转，当∠BAC为钝角时，如图③，CA的延长线与⊙O相交于E．
请问：∠BAC与∠CBE的关系是否与(2)中你得出的关系相同？若相同，请加以证明；若不同，请说明理由．
查看习题详情和答案>>
25、如图，在锐角△ABC中，AB＞AC，AD⊥BC于D，以AD为直径的⊙O分别交AB，AC于E，F，连接DE，DF．（1）求证：∠EAF+∠EDF=180°；
（2）已知P是射线DC上一个动点，当点P运动到PD=BD时，连接AP，交⊙O于G，连接DG．设∠EDG=∠α，∠APB=∠β，那么∠α与∠β有何数量关系？试证明你的结论．[在探究∠α与∠β的数量关系时，必要时可直接运用（1）的结论进行推理与解答]
