摘要:17.解:(Ⅰ)因为函数为奇函数.所以.对任意的..即.又所以.所以解得.得.所以.当时.由得.变化时.的变化情况如下表:00 所以.当时.函数在上单调递增.在上单调递减.在上单调递增.当时..所以函数在上单调递增.
网址:http://m.1010jiajiao.com/timu_id_68338[举报]
(本小题共13分)
已知数列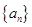 的前
的前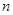 项和为
项和为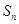 ,且
,且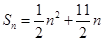 .
.
数列 满足
满足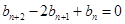 (
( ),且
),且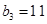 ,
, .
.
(Ⅰ)求数列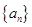 ,
, 的通项公式;
的通项公式;
(Ⅱ)设 ,数列
,数列 的前
的前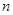 项和为
项和为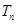 ,求使不等式
,求使不等式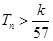 对一切
对一切 都成立的最大正整数
都成立的最大正整数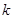 的值;
的值;
(Ⅲ)设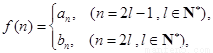 是否存在
是否存在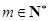 ,使得
,使得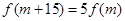 成立?若存在,求出
成立?若存在,求出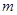 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
查看习题详情和答案>>
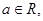 函数
函数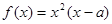 .
.
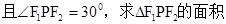 .
.