摘要:(Ⅲ)求λ的取值范围.使得存在正整数m,当n>m时总有an<0. 2008年普通高等学校招生全国统一考试北京文数全解全析本试卷分第Ⅰ卷和第Ⅱ卷两部分.第Ⅰ卷1至2页.第Ⅱ卷3至9页.共150分.考试时间120分钟.考试结束.将本试卷和答题卡一并交回. 第Ⅰ卷注意事项:
网址:http://m.1010jiajiao.com/timu_id_68316[举报]
已知函数 ,
, .
.
(Ⅰ)若函数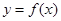 依次在
依次在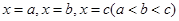 处取到极值.求
处取到极值.求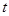 的取值范围;
的取值范围;
(Ⅱ)若存在实数 ,使对任意的
,使对任意的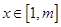 ,不等式
,不等式
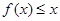 恒成立.求正整数
恒成立.求正整数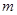 的最大值.
的最大值.
【解析】第一问中利用导数在在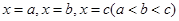 处取到极值点可知导数为零可以解得方程有三个不同的实数根来分析求解。
处取到极值点可知导数为零可以解得方程有三个不同的实数根来分析求解。
第二问中,利用存在实数 ,使对任意的
,使对任意的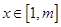 ,不等式
,不等式
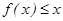 恒成立转化为
恒成立转化为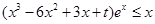 ,恒成立,分离参数法求解得到范围。
,恒成立,分离参数法求解得到范围。
解:(1)
①

(2)不等式 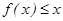 ,即
,即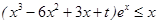 ,即
,即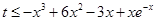 .
.
转化为存在实数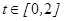 ,使对任意的
,使对任意的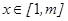 ,不等式
,不等式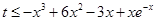 恒成立.
恒成立.
即不等式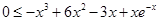 在
在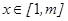 上恒成立.
上恒成立.
即不等式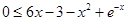 在
在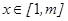 上恒成立.
上恒成立.
设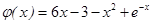 ,则.
,则.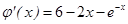
设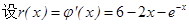 ,则
,则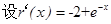 ,因为
,因为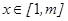 ,有
,有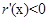 .
.
故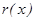 在区间
在区间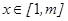 上是减函数。又
上是减函数。又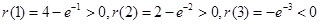
故存在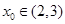 ,使得
,使得 .
.
当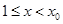 时,有
时,有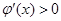 ,当
,当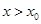 时,有
时,有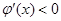 .
.
从而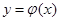 在区间
在区间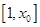 上递增,在区间
上递增,在区间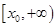 上递减.
上递减.
又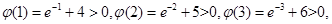 [来源:]
[来源:]
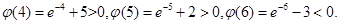
所以当 时,恒有
时,恒有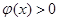 ;当
;当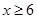 时,恒有
时,恒有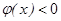
 ;
;
故使命题成立的正整数m的最大值为5
查看习题详情和答案>>
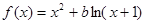 ,其中
,其中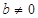 .
.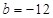 ,求
,求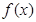 在
在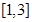 上的最小值;
上的最小值;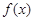 在定义域内既有极大值又有极小值,求实数
在定义域内既有极大值又有极小值,求实数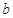 的取值范围;
的取值范围;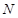 ,使得当
,使得当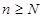 时,不等式
时,不等式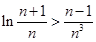 恒成立.
恒成立. ,其中
,其中 .(Ⅰ)若
.(Ⅰ)若 ,求
,求 在
在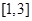 上的最小值;
上的最小值; 在定义域内既有极大值又有极小值,求实数
在定义域内既有极大值又有极小值,求实数 的取值范围;
的取值范围; ,使得当
,使得当 时,不等式
时,不等式 恒成立.
恒成立. ,其中
,其中 .(Ⅰ)若
.(Ⅰ)若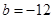 ,求
,求 在
在 上的最小值;
上的最小值; 在定义域内既有极大值又有极小值,求实数
在定义域内既有极大值又有极小值,求实数 的取值范围;
的取值范围; ,使得当
,使得当 时,不等式
时,不等式 恒成立.
恒成立.