摘要:14.观察下列分式....--
网址:http://m.1010jiajiao.com/timu_id_682631[举报]
17、观察下列等式,解答下列问题
等式(1):32+42=52
等式(2):102+112+122=132+142
等式(3):212+222+232+242=252+262+272
…
等式(n)
(1)由上述等式可知,每个等式中紧靠等于号左边的数分别是42、122、242…,这些数存在规律(4×1)2,[4×(1+2)]2,[4×(1+2+3)]2…请你根据这个规律直接写出等式(4);
(2)若紧靠等于号左边的数是2202,那么该等式是多少个连续正整数平方和组成的?
查看习题详情和答案>>
等式(1):32+42=52
等式(2):102+112+122=132+142
等式(3):212+222+232+242=252+262+272
…
等式(n)
(1)由上述等式可知,每个等式中紧靠等于号左边的数分别是42、122、242…,这些数存在规律(4×1)2,[4×(1+2)]2,[4×(1+2+3)]2…请你根据这个规律直接写出等式(4);
(2)若紧靠等于号左边的数是2202,那么该等式是多少个连续正整数平方和组成的?
观察下列图形:
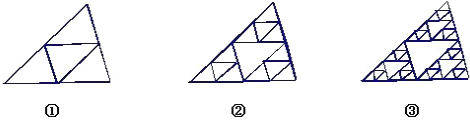
如果按这个规律一直排到第n个图形,请探究下列问题:
(1)设第n个图形和第n-1个图形中所有三角形的个数分别为an、an-1,问:它们之间有什么数量关系?请写出这个关系式.
(2)请你用含n的代数式来表示an,并证明你的结论. 查看习题详情和答案>>

如果按这个规律一直排到第n个图形,请探究下列问题:
(1)设第n个图形和第n-1个图形中所有三角形的个数分别为an、an-1,问:它们之间有什么数量关系?请写出这个关系式.
(2)请你用含n的代数式来表示an,并证明你的结论. 查看习题详情和答案>>
观察下列图形,根据图①、②、③的规律,若图①为第1次分割,图②为第2次分割,图③为第3次分割,按照这个规律一直分割下去,进行了n(n≥1)次分割,图中一共有
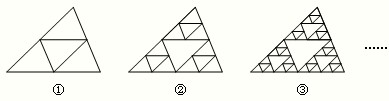
查看习题详情和答案>>
2×3n-1
2×3n-1
个三角形(用含n的代数式表示).
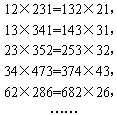
 ,个位数字为
,个位数字为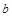 ,且2≤
,且2≤ ≤9,写出表示“数字对称等式”一般规律的式子(含
≤9,写出表示“数字对称等式”一般规律的式子(含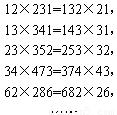
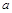 ,个位数字为
,个位数字为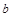 ,且2≤
,且2≤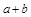 ≤9,写出表示“数字对称等式”一般规律的式子(含
≤9,写出表示“数字对称等式”一般规律的式子(含