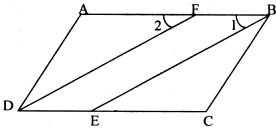
摘要：已知:如图.∠ADC=∠ABC.BE.DF分别平分∠ABC.∠ADC.且∠1=∠2．求证:∠A=∠C．
网址：http://m.1010jiajiao.com/timu_id_680306[举报]
13、
（Ⅰ）已知：如图，平行四边形ABCD的对角线AC、BD相交于点O，EF过点O与AB、CD分别相交于点E、F．求证：BE=DF．
（Ⅱ）请写出使如图所示的四边形ABCD为平行四边形的条件（例如，填：AB∥CD且AD∥BC．在不添加辅助线的情况下，写出除上述条件外的另外四组条件，将答案直接写在下面的横线上．）
（1）：
∠DAB=∠DCB且∠ADC=∠ABC
；（2）：
AB=CD且AD=BC
；（3）：
OA=OC且OD=OB
；（4）：
AB∥CD且∠DAB=∠DCB
．
如图，已知，∠ADC=∠ABC，BE、DF分别平分∠ABC、∠ADC，且∠1=∠2．求证：∠A=∠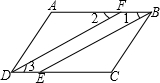
C．
证明：∵BE、DF分别平分∠ABC、∠ADC（已知）
∴∠1=
∠ABC，∠3=
∠ADC（ ）
∵∠ABC=∠ADC（已知）
∴
∠ABC=
∠ADC（ ）
∴∠1=∠3（ ）
∵∠1=∠2（已知）
∴∠2=∠3（等量代换）
∴（ ）∥（ ）（ ）
∴∠A+∠ =180°，∠C+∠ =180°（ ）
∴∠A=∠C（等量代换）． 查看习题详情和答案>>
C．证明：∵BE、DF分别平分∠ABC、∠ADC（已知）
∴∠1=
| 1 |
| 2 |
| 1 |
| 2 |
∵∠ABC=∠ADC（已知）
∴
| 1 |
| 2 |
| 1 |
| 2 |
∴∠1=∠3（
∵∠1=∠2（已知）
∴∠2=∠3（等量代换）
∴（
∴∠A+∠
∴∠A=∠C（等量代换）． 查看习题详情和答案>>
如图，已知，∠ADC=∠ABC，BE、DF分别平分∠ABC、∠ADC，且∠1=∠2．求证：∠A=∠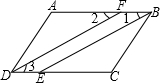
C．
证明：∵BE、DF分别平分∠ABC、∠ADC（已知）
∴∠1=
∠ABC，∠3=∠ADC（________）
∵∠ABC=∠ADC（已知）
∴∠ABC=∠ADC（________）
∴∠1=∠3（________）
∵∠1=∠2（已知）
∴∠2=∠3（等量代换）
∴（________）∥（________）（________）
∴∠A+∠________=180°，∠C+∠________=180°（________）
∴∠A=∠C（等量代换）．
查看习题详情和答案>>
填写推理的依据．
（1）已知：如图1，AB∥CD，AD∥BC．求证：∠B=∠D．
证明：∵AB∥CD，AD∥BC（已知）
∴∠A+∠B=180°，∠A+∠D=180°
∴∠B=∠D
（2）已知：如图2，DF∥AC，∠A=∠F．求证：AE∥BF．
证明：∵DF∥AC （已知）
∴∠FBC=∠
∵∠A=∠F（已知）
∴∠A=∠FBC
∴AE∥FB
（3）已知：如图3，∠ADC=∠ABC，BE、DF分别平分∠ABC、∠ADC，且∠1=∠2
求证：∠A=∠C．
证明：∵BE、DF分别平分∠ABC、∠ADC（已知）
∴∠1=
∠ABC，∠3=
∠ADC
∵∠ABC=∠ADC（已知）
∴
∠ABC=
∠ADC
∴∠1=∠3
∵∠1=∠2（已知）
∴∠2=∠3
∴ ∥
∴∠A+∠ =180°，∠C+∠ =180°
∴∠A=∠C（等量代换）
查看习题详情和答案>>
（1）已知：如图1，AB∥CD，AD∥BC．求证：∠B=∠D．
证明：∵AB∥CD，AD∥BC（已知）
∴∠A+∠B=180°，∠A+∠D=180°
∴∠B=∠D
（2）已知：如图2，DF∥AC，∠A=∠F．求证：AE∥BF．
证明：∵DF∥AC （已知）
∴∠FBC=∠
∵∠A=∠F（已知）
∴∠A=∠FBC
∴AE∥FB
（3）已知：如图3，∠ADC=∠ABC，BE、DF分别平分∠ABC、∠ADC，且∠1=∠2
求证：∠A=∠C．
证明：∵BE、DF分别平分∠ABC、∠ADC（已知）
∴∠1=
| 1 |
| 2 |
| 1 |
| 2 |
∵∠ABC=∠ADC（已知）
∴
| 1 |
| 2 |
| 1 |
| 2 |
∴∠1=∠3
∵∠1=∠2（已知）
∴∠2=∠3
∴
∴∠A+∠
∴∠A=∠C（等量代换）
查看习题详情和答案>>