网址:http://m.1010jiajiao.com/timu_id_679010[举报]
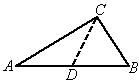
(2006重庆课改,28)(10分)如图1所示,一张三角形纸片ABC,∠ACB=90°,AC=8,BC=6.沿斜边AB的中线CD把这张纸片剪成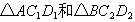 两个三角形(如图2所示).将纸片
两个三角形(如图2所示).将纸片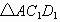 沿直线
沿直线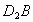 (AB)方向平移(点A,
(AB)方向平移(点A,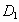 ,
, ,B始终在同一条直线上),当点
,B始终在同一条直线上),当点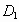 与点B重合时,停止平移.在平移的过程中,
与点B重合时,停止平移.在平移的过程中,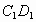 与
与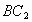 交于点E,
交于点E,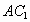 与
与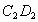 、
、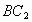 分别交于点F、P.
分别交于点F、P.
|
图1 |
图2 |
(1)当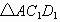 平移到如图3所示的位置时,猜想图中
平移到如图3所示的位置时,猜想图中 的数量关系,并证明你的猜想;
的数量关系,并证明你的猜想;
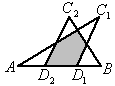
图3
(2)设平移距离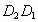 为x,
为x,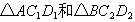 重叠部分的面积为y,请写出y与x的函数关系式,以及自变量x的取值范围;
重叠部分的面积为y,请写出y与x的函数关系式,以及自变量x的取值范围;
(3)对于(2)中结论是否存在这样的x,使得重叠部分面积等于原△ABC纸片面积的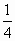 ?若存在,请求出x的值;若不存在,请说明理由.
?若存在,请求出x的值;若不存在,请说明理由.
课题研究:现有边长为120厘米的正方形铁皮,准备将它设计并制成一个开口的水槽,使水槽能通过的水的流量最大.初三(1)班数学兴趣小组经讨论得出结论:在水流速度一定的情况下,水槽的横截面面积越大,则通过水槽的水的流量越大.为此,他们对水槽的横截面进行了如下探索:
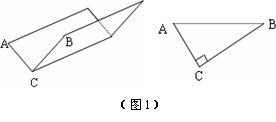
⑴方案①:把它折成横截面为直角三角形的水槽(如图1).
若∠ACB=90°,设AC=x厘米,该水槽的横截面面积为y厘米2,请你写出y关于x的函数关系式(不必写出x的取值范围),并求出当x取何值时,y的值最大,最大值又是多少?
 |
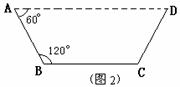
方案②:把它折成横截面为等腰梯形的水槽(如图2).
若∠ABC=120°,请你求出该水槽的横截面面积的最大值,并与方案①中的y的最大值比较大小.
 |
⑵假如你是该兴趣小组中的成员,请你再提供两种方案,使你所设计的水槽的横截面面积更大.画出你设计的草图,标上必要的数据(不要求写出解答过程).(习题改编)
查看习题详情和答案>>