题目内容
(2006重庆课改,28)(10分)如图1所示,一张三角形纸片ABC,∠ACB=90°,AC=8,BC=6.沿斜边AB的中线CD把这张纸片剪成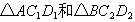 两个三角形(如图2所示).将纸片
两个三角形(如图2所示).将纸片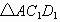 沿直线
沿直线 (AB)方向平移(点A,
(AB)方向平移(点A, ,
, ,B始终在同一条直线上),当点
,B始终在同一条直线上),当点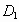 与点B重合时,停止平移.在平移的过程中,
与点B重合时,停止平移.在平移的过程中,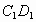 与
与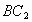 交于点E,
交于点E,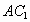 与
与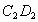 、
、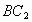 分别交于点F、P.
分别交于点F、P.
|
图1 |
图2 |
(1)当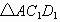 平移到如图3所示的位置时,猜想图中
平移到如图3所示的位置时,猜想图中 的数量关系,并证明你的猜想;
的数量关系,并证明你的猜想;
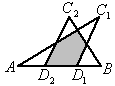
图3
(2)设平移距离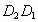 为x,
为x,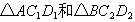 重叠部分的面积为y,请写出y与x的函数关系式,以及自变量x的取值范围;
重叠部分的面积为y,请写出y与x的函数关系式,以及自变量x的取值范围;
(3)对于(2)中结论是否存在这样的x,使得重叠部分面积等于原△ABC纸片面积的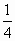 ?若存在,请求出x的值;若不存在,请说明理由.
?若存在,请求出x的值;若不存在,请说明理由.
答案:略
解析:
解析:
|
(1) 因为 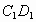 ∥ ∥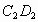 ,所以 ,所以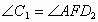 . .
又因为∠ ACB=90°,CD是斜边AB的中线,所以 DC=DA=DB,即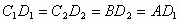 . .
所以 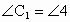 ,所以 ,所以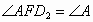 .(2分) .(2分)
所以 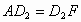 .同理: .同理: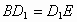 . .
又因为 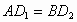 ,所以 ,所以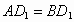 .所以 .所以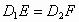 .(3分) .(3分)
(2)因为在RtΔABC中,AC=8,BC=6,所以由勾股定理,得AB=10.即 又因为
在 设 所以 又因为 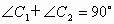 ,所以 ,所以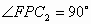 . .
又因为  . .
所以 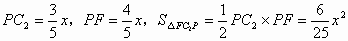 .(7分) .(7分)
而  . .
所以 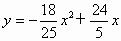 (0≤x≤5).(8分) (0≤x≤5).(8分)
(3)存在.当 整理,得 即当 |

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目

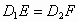 .(1分)
.(1分)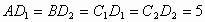 .
.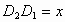 ,所以
,所以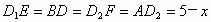 .所以
.所以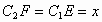 .
.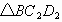 中,
中,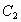 到
到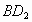 的距离就是ΔABC的AB边上的高,为
的距离就是ΔABC的AB边上的高,为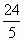 .
.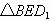 的
的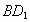 边上的高为h,由探究,得
边上的高为h,由探究,得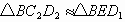 ,所以
,所以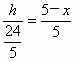 .
.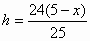 .
. .(5分)
.(5分)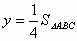 时,即
时,即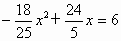 .
.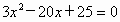 .解得,
.解得,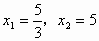 .
.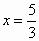 或x=5时,重叠部分面积等于原ΔABC面积的
或x=5时,重叠部分面积等于原ΔABC面积的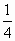 .(10分)
.(10分)
 ,∠1=40°,那么∠2=________度.
,∠1=40°,那么∠2=________度.
 ,
, ,
, ,
, ,
, ,
, ……,按此规律排列下去,这列数中的第7个数是________.
……,按此规律排列下去,这列数中的第7个数是________. 春节期间,这三种不同包装的土特产都销售了12 000千克,那么本次销售中,这三种包装的土特产获得利润最大的是
春节期间,这三种不同包装的土特产都销售了12 000千克,那么本次销售中,这三种包装的土特产获得利润最大的是