摘要:当时,不存在.即不存在这样的直线 .12分
网址:http://m.1010jiajiao.com/timu_id_67780[举报]
(2013•蓟县二模)已知函数f(x)=-
x3+
(2a+1)x2-2ax+1,其中a为实数.
(Ⅰ)当a≠
时,求函数f(x)的极大值点和极小值点;
(Ⅱ) 若对任意a∈(2,3)及x∈[1,3]时,恒有ta2-f(x)>
成立,求实数t的取值范围.
(Ⅲ)已知g(x)=a2x2+ax+1,m(x)=
x3-(a2+
)x2+(2a+5)x-3,h(x)=f(x)+m(x),设函数q(x)=
是否存在a,对任意给定的非零实数x1,存在惟一的非零实数x2(x2≠x1),使得q′(x2)=q′(x1)成立?若存在,求a的值;若不存,请说明理由.
查看习题详情和答案>>
| 1 |
| 3 |
| 1 |
| 2 |
(Ⅰ)当a≠
| 1 |
| 2 |
(Ⅱ) 若对任意a∈(2,3)及x∈[1,3]时,恒有ta2-f(x)>
| 3 |
| 2 |
(Ⅲ)已知g(x)=a2x2+ax+1,m(x)=
| 4 |
| 3 |
| 3 |
| 2 |
|
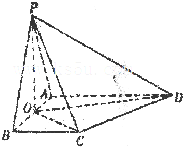 如图,在四棱锥P-ABCD中,平面PAB⊥平面ABCD,AD∥BC,∠ABC=90°,PA=PB=3,BC=1,AB=2,AD=3,O是AB中点.
如图,在四棱锥P-ABCD中,平面PAB⊥平面ABCD,AD∥BC,∠ABC=90°,PA=PB=3,BC=1,AB=2,AD=3,O是AB中点.(Ⅰ)证明CD⊥平面POC;
(Ⅱ)求二面角C-PD-O的平面角的余弦值.
(Ⅲ)在侧棱PC上是否存在点M,使得BM∥平面POD,若存在试求出
| CM | PC |
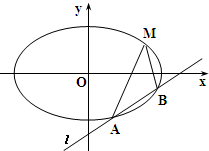 如图,已知焦点在x轴上的椭圆
如图,已知焦点在x轴上的椭圆| x2 |
| 20 |
| y2 |
| b2 |
(1)求该椭圆的标准方程;
(2)求实数m的取值范围;
(3)是否存在实数m,使△ABM为直角三角形,若存在,求出m的值,若不存,请说明理由. 查看习题详情和答案>>
 ,
, 为实数)有极值,且在
为实数)有极值,且在 处的切线与直线
处的切线与直线 平行.
平行. 的极小值为1,若存在,求出实数a的值;若不存
的极小值为1,若存在,求出实数a的值;若不存
 .
. ,
, R.
R.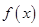 的单调区间;
的单调区间; ,使得函数
,使得函数 ?若存在,求
?若存在,求