摘要:5.已知的图像是抛物线.若抛物线不动.把轴.轴分别向上.向右平移2个单位.那么在新坐标系下抛物线的解析式是
网址:http://m.1010jiajiao.com/timu_id_677659[举报]
已知一次函数y1 =2x和二次函数y2 = x2 + 1。
1.求证:函数y1、y2的图像都经过同一个定点;
2.求证:在实数范围内,对于任意同一个x的值,这两个函数所对应的函数值y1 ≤ y2 总成立;
3.是否存在抛物线y3 = ax2 + bx + c,其图象经过点(![]() 5,2),且在实数范围内,对于同一个x的值,这三个函数所对应的函数值y1 ≤ y3 ≤ y2总成立?若存在,求出y3的解析式;若不存在,说明理由。
5,2),且在实数范围内,对于同一个x的值,这三个函数所对应的函数值y1 ≤ y3 ≤ y2总成立?若存在,求出y3的解析式;若不存在,说明理由。
查看习题详情和答案>>
已知一次函数y1 = 2x和二次函数y2 = x2 + 1。
【小题1】求证:函数y1、y2的图像都经过同一个定点;
【小题2】求证:在实数范围内,对于任意同一个x的值,这两个函数所对应的函数值y1 ≤ y2总成立;
【小题3】是否存在抛物线y3 = ax2 + bx + c,其图象经过点( 5,2),且在实数范围内,对于同一个x的值,这三个函数所对应的函数值y1 ≤ y3 ≤ y2总成立?若存在,求出y3的解析式;若不存在,说明理由。
查看习题详情和答案>>
5,2),且在实数范围内,对于同一个x的值,这三个函数所对应的函数值y1 ≤ y3 ≤ y2总成立?若存在,求出y3的解析式;若不存在,说明理由。
查看习题详情和答案>>
【小题1】求证:函数y1、y2的图像都经过同一个定点;
【小题2】求证:在实数范围内,对于任意同一个x的值,这两个函数所对应的函数值y1 ≤ y2总成立;
【小题3】是否存在抛物线y3 = ax2 + bx + c,其图象经过点(
 5,2),且在实数范围内,对于同一个x的值,这三个函数所对应的函数值y1 ≤ y3 ≤ y2总成立?若存在,求出y3的解析式;若不存在,说明理由。
查看习题详情和答案>>
5,2),且在实数范围内,对于同一个x的值,这三个函数所对应的函数值y1 ≤ y3 ≤ y2总成立?若存在,求出y3的解析式;若不存在,说明理由。
查看习题详情和答案>>
已知一次函数y1 = 2x和二次函数y2 = x2 + 1。
【小题1】求证:函数y1、y2的图像都经过同一个定点;
【小题2】求证:在实数范围内,对于任意同一个x的值,这两个函数所对应的函数值y1 ≤ y2总成立;
【小题3】是否存在抛物线y3 = ax2 + bx + c,其图象经过点(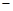 5,2),且在实数范围内,对于同一个x的值,这三个函数所对应的函数值y1 ≤ y3 ≤ y2总成立?若存在,求出y3的解析式;若不存在,说明理由。
5,2),且在实数范围内,对于同一个x的值,这三个函数所对应的函数值y1 ≤ y3 ≤ y2总成立?若存在,求出y3的解析式;若不存在,说明理由。
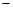 5,2),且在实数范围内,对于同一个x的值,这三个函数所对应的函数值y1 ≤ y3 ≤ y2总成立?若存在,求出y3的解析式;若不存在,说明理由。
5,2),且在实数范围内,对于同一个x的值,这三个函数所对应的函数值y1 ≤ y3 ≤ y2总成立?若存在,求出y3的解析式;若不存在,说明理由。