题目内容
已知一次函数y1 = 2x和二次函数y2 = x2 + 1。
1.求证:函数y1、y2的图像都经过同一个定点;
2.求证:在实数范围内,对于任意同一个x的值,这两个函数所对应的函数值y1 ≤ y2 总成立;
3.是否存在抛物线y3 = ax2 + bx + c,其图象经过点(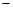 5,2),且在实数范围内,对于同一个x的值,这三个函数所对应的函数值y1 ≤ y3 ≤ y2总成立?若存在,求出y3的解析式;若不存在,说明理由。
5,2),且在实数范围内,对于同一个x的值,这三个函数所对应的函数值y1 ≤ y3 ≤ y2总成立?若存在,求出y3的解析式;若不存在,说明理由。
【答案】
1.如果经过同一点,那么y1=y2,即2x= x2 + 1
x=1
把x=1代入到一次函数中得 y=2
∴函数y1、y2的图像都经过同一个定点(1,2)(3分)
2.∵y2- y1= x2 + 1-2x= (x-1)2≥0
∴在实数范围内,对于任意同一个x的值,这两个函数所对应的函数值y1 ≤ y2 总成立;(3分)
3.存在
∵三个函数所对应的函数值y1 ≤ y3 ≤ y2总成立
∴抛物线y3 = ax2 + bx + c也必经(1,2)
把(1,2)和(-5,2)代入抛物线y3 = ax2 + bx + c中解得:
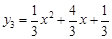 (4分)
(4分)
【解析】(1)利用y1=y2,求出定点的坐标从而得证;
(2)求出y2- y1关于x的方程进行变形讨论出结论;
(3)要符合y1 ≤ y3 ≤ y2条件,就必然得出抛物线y3 = ax2 + bx + c也必经(1,2),然后把(1,2)和(-5,2)代入就得出解析式。

练习册系列答案
 捷径训练检测卷系列答案
捷径训练检测卷系列答案 小夫子全能检测系列答案
小夫子全能检测系列答案
相关题目
 2,4)、(4,-2).
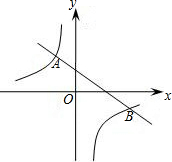
2,4)、(4,-2). (2012•德阳)已知一次函数y1=x+m的图象与反比例函数
(2012•德阳)已知一次函数y1=x+m的图象与反比例函数 已知一次函数y1=ax+b的图象与反比例函数y2=
已知一次函数y1=ax+b的图象与反比例函数y2= 如图所示,已知一次函数y1=kx+b的图象经过A(1,2)、B(-1,0)两点,y2=mx+n的图象经过A、C(3,0)两点,则不等式组0<kx+b<mx+n的解集是( )
如图所示,已知一次函数y1=kx+b的图象经过A(1,2)、B(-1,0)两点,y2=mx+n的图象经过A、C(3,0)两点,则不等式组0<kx+b<mx+n的解集是( )