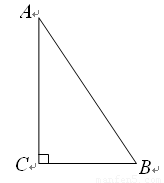
摘要:八.25.如图所示.在直角坐标系中.矩形ABCD的边AD在X轴上. 点A在坐标原点.AB=3.AD=5,若矩形以每秒2个单位长度沿轴正方向作匀速运动.同时点P从A点 出发以每秒1个单位长度沿A―B―C―D的路线作匀速运动.当P点运动到D点时停止运动.矩形ABCD也随之停止运动.(1) 求P点从A点运动到D点所需的时间.(2) 设P点运动的时间为t(秒). ①当t=5时.求出点P的坐标. ②若△OAP的面积为S.试求出S与t之间的函数关系式(并写出相应的自变量的取值范围).
网址:http://m.1010jiajiao.com/timu_id_676363[举报]
(本题满分12分)
如图所示,在平面直角坐标系中,顶点为(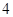 ,
,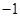 )的抛物线交
)的抛物线交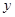 轴于
轴于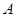 点,交
点,交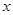 轴于
轴于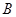 ,
,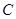 两点(点
两点(点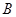 在点
在点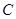 的左侧), 已知
的左侧), 已知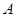 点坐标为(
点坐标为( ,
,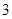 ).
).
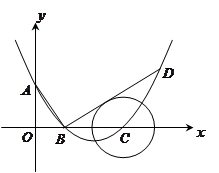
(1)求此抛物线的解析式;
(2)过点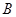 作线段
作线段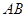 的垂线交抛物线于点
的垂线交抛物线于点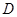 ,
,
如果以点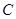 为圆心的圆与直线
为圆心的圆与直线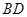 相切,请判断抛物
相切,请判断抛物
线的对称轴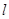 与⊙
与⊙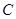 有怎样的位置关系,并给出证明;
有怎样的位置关系,并给出证明;
(3)已知点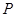 是抛物线上的一个动点,且位于
是抛物线上的一个动点,且位于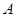 ,
,
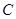 两点之间,问:当点
两点之间,问:当点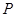 运动到什么位置时,
运动到什么位置时,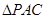 的
的
面积最大?并求出此时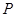 点的坐标和
点的坐标和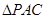 的最大面积.
查看习题详情和答案>>
的最大面积.
查看习题详情和答案>>
如图所示,在平面直角坐标系中,顶点为(
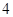 ,
,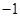 )的抛物线交
)的抛物线交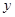 轴于
轴于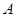 点,交
点,交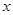 轴于
轴于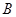 ,
,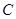 两点(点
两点(点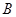 在点
在点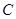 的左侧), 已知
的左侧), 已知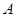 点坐标为(
点坐标为( ,
,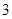 ).
).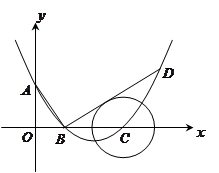
(1)求此抛物线的解析式;
(2)过点
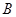 作线段
作线段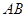 的垂线交抛物线于点
的垂线交抛物线于点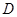 ,
,如果以点
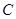 为圆心的圆与直线
为圆心的圆与直线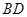 相切,请判断抛物
相切,请判断抛物线的对称轴
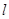 与⊙
与⊙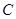 有怎样的位置关系,并给出证明;
有怎样的位置关系,并给出证明;(3)已知点
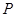 是抛物线上的一个动点,且位于
是抛物线上的一个动点,且位于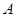 ,
,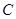 两点之间,问:当点
两点之间,问:当点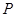 运动到什么位置时,
运动到什么位置时,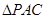 的
的面积最大?并求出此时
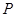 点的坐标和
点的坐标和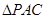 的最大面积.
查看习题详情和答案>>
的最大面积.
查看习题详情和答案>>
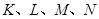 ,使
,使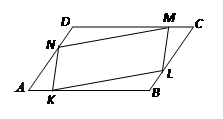
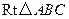 中,
中, .
.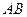 的垂直平分线
的垂直平分线 (保留作图痕迹,不写作法);
(保留作图痕迹,不写作法); 及
及 的延长线于点
的延长线于点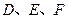 ,连接
,连接 .求证:
.求证: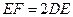 .
.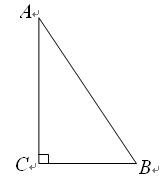
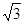 ,矩形ABOC绕点O按顺时针方向旋转60°后得矩形EFOD. 点A的对应点为点E,点B的对应点为F,点C的对应点为点D. 抛物线
,矩形ABOC绕点O按顺时针方向旋转60°后得矩形EFOD. 点A的对应点为点E,点B的对应点为F,点C的对应点为点D. 抛物线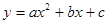 过点A、E、D.
过点A、E、D.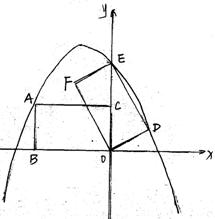
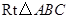 中,
中,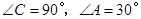 .
.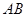 的垂直平分线
的垂直平分线 (保留作图痕迹,不写作法);
(保留作图痕迹,不写作法); 及
及 的延长线于点
的延长线于点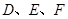 ,连接
,连接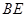 .求证:
.求证: .
.