摘要:中你归纳的数学关系式.解释下面生活中的一个现象:“若克糖水里含有克糖.再加入克糖.则糖水更甜了 ,
网址:http://m.1010jiajiao.com/timu_id_676167[举报]
(1)比较下列各组数的大小,找规律,提出你的猜想:
 ______
______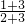 ;
;  ______
______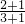 ;
;  ______
______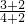 ;
;  ______
______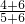 ;
;  ______
______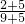 ;
; 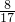 ______
______ 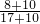 .
.
从上面的各式发现一个正分数的分子和分母______,所得分数的值比原分数的值要______.
猜想:设a>b>0,m>0,则 ______
______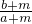 .
.
(2)试证明你的猜想:
(3)试用(1)中你归纳的数学关系式,解释下面生活中的一个现象:“若m克糖水里含有n克糖,再加入k克糖(仍不饱和),则糖水更甜了”.
查看习题详情和答案>>
(1)比较下列各组数的大小,找规律,提出你的猜想:
;
;
;
;
;
.
从上面的各式发现一个正分数的分子和分母
猜想:设a>b>0,m>0,则
.
(2)试证明你的猜想:
(3)试用(1)中你归纳的数学关系式,解释下面生活中的一个现象:“若m克糖水里含有n克糖,再加入k克糖(仍不饱和),则糖水更甜了”.
查看习题详情和答案>>
| 1 |
| 2 |
<
<
| 1+3 |
| 2+3 |
| 2 |
| 3 |
<
<
| 2+1 |
| 3+1 |
| 3 |
| 4 |
<
<
| 3+2 |
| 4+2 |
| 4 |
| 5 |
<
<
| 4+6 |
| 5+6 |
| 2 |
| 9 |
<
<
| 2+5 |
| 9+5 |
| 8 |
| 17 |
<
<
| 8+10 |
| 17+10 |
从上面的各式发现一个正分数的分子和分母
都加上同一个正数
都加上同一个正数
,所得分数的值比原分数的值要大
大
.猜想:设a>b>0,m>0,则
| b |
| a |
<
<
| b+m |
| a+m |
(2)试证明你的猜想:
(3)试用(1)中你归纳的数学关系式,解释下面生活中的一个现象:“若m克糖水里含有n克糖,再加入k克糖(仍不饱和),则糖水更甜了”.
在数学学习过程中,通常是利用已有的知识与经验,通过对研究对象进行观察、实验、推理、抽象概括,发现数学规律,揭示研究对象的本质特征.
比如撏?资?莸某朔ǚㄔ驍的学习过程是利用有理数的乘方概念和乘法结合律,由撎厥鈹到撘话銛进行抽象概括的:![]() ,
,![]() ,
,![]() ,
,![]()
![]() ,
,
![]()
![]()
我们亦知:![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() .
.
(1
)请你根据上面的材料归纳出(2
)试用(1)中你归纳的数学关系式,解释下面生活中的一个现象:撊-(3
)如图,在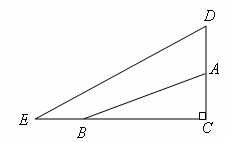
在数学学习过程中,通常是利用已有的知识与经验,通过对研究对象进行观察、实验、推理、抽象概括,发现数学规律,揭示研究对象的本质特征。比如“同底数幂的乘法法则”的学习过程是利用有理数的乘方概念和乘法结合律,由“特殊”到“一般”进行抽象概括的: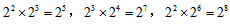
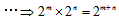 ,
,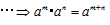 (m、n都是正整数),我们亦知:
(m、n都是正整数),我们亦知: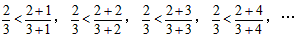
(1)请你根据上面的材料归纳出a、b、c(a>b>0,c>0)之间的一个数学关系式;
(2)试用(1)中你归纳的数学关系式,解释下面生活中的一个现象:“若m克糖水里含有n克糖,再加入k克糖(仍不饱和),则糖水更甜了”;
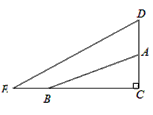
(3)如图,在Rt△ABC中,∠C=90°,CB=a,CA=b,AD=BE=c(a>b),能否根据这个图形提炼出与(1)中相同的关系式并给予证明。
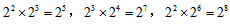
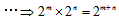 ,
,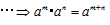 (m、n都是正整数),我们亦知:
(m、n都是正整数),我们亦知: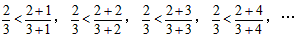
(1)请你根据上面的材料归纳出a、b、c(a>b>0,c>0)之间的一个数学关系式;
(2)试用(1)中你归纳的数学关系式,解释下面生活中的一个现象:“若m克糖水里含有n克糖,再加入k克糖(仍不饱和),则糖水更甜了”;
(3)如图,在Rt△ABC中,∠C=90°,CB=a,CA=b,AD=BE=c(a>b),能否根据这个图形提炼出与(1)中相同的关系式并给予证明。
在数学学习过程中,通常是利用已有的知识与经验,通过对研究对象进行观察、实验、推理、抽象概括,发现数学规律,揭示研究对象的本质特征.
比如“同底数幂的乘法法则”的学习过程是利用有理数的乘方概念和乘法结合律,由“特殊”到“一般”进行抽象概括的:22×23=25,23×24=27,22×26=28,…![]() 2m×2n=2m+n,…
2m×2n=2m+n,…![]() am×an=am+n(m,n都是正整数).
am×an=am+n(m,n都是正整数).
我们亦知:![]() ,
,![]() ,
,![]() ,
,![]() ,….
,….
(1)请你根据上面的材料归纳出a,b,c(a>b>0,c>0)之间的一个数学关系式;
(2)试用(1)中你归纳的数学关系式,解释下面生活中的一个现象:“若m克糖水里含有n克糖,再加入k克糖(仍不饱和),则糖水更甜了”;
(3)如图,在Rt△ABC中,∠C=90°,CB=a,CA=b,AD=BE=c(a>b).能否根据这个图形提炼出与(1)中同样的关系式?并给予证明.
