摘要：已知:如图13.在△ABC中.D为AB边上一点.∠A=36º.AC=BC.AC＝AB?AD． (1)试说明:△ADC和△BDC都是等腰三角形, (2)若AB=1.求AC的值, (3)试构造一个等腰梯形.该梯形连同它的两条对角线.得到了8个三角形.要求构造出的图形中有尽可能多的等腰三角形．
网址：http://m.1010jiajiao.com/timu_id_675001[举报]
已知：如图，△ABC中，AB=AC=6，cosB=
，⊙O的半径为OB，圆心在AB上，且分别与边AB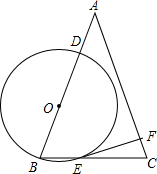
、BC相交于D、E两点，但⊙O与边AC不相交，又EF⊥AC，垂足为F．设OB=x，CF=y．
（1）判断直线EF与⊙O的位置关系，并说明理由；
（2）设OB=x，CF=y．
①求y关于x的函数关系式；
②当直线DF与⊙O相切时，求OB的长． 查看习题详情和答案>>
| 1 | 3 |
、BC相交于D、E两点，但⊙O与边AC不相交，又EF⊥AC，垂足为F．设OB=x，CF=y．（1）判断直线EF与⊙O的位置关系，并说明理由；
（2）设OB=x，CF=y．
①求y关于x的函数关系式；
②当直线DF与⊙O相切时，求OB的长． 查看习题详情和答案>>
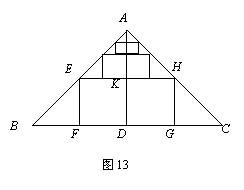
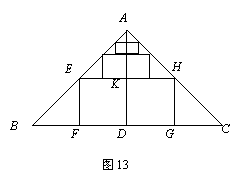
已知：如图13，等腰△ABC中，底边BC=12，高AD=6．
（1）在△ABC内作矩形EFGH，使F、G在BC上，E、H分别在AB、AC上，且长是宽的2倍．求矩形EFGH的面积．
（2）在（1）的基础上，再作第二个矩形，使其两个顶点在EH上，另外两个顶点分别在AB、AC上，且长是宽的2倍．则第二个矩形的面积为 ；
（3）在（2）的基础上，再作第三个矩形，使其两个顶点在第二个矩形的边上，另外两个顶点分别在AB、AC上，且长是宽的2倍．则第三个矩形的面积为 ；
（4）按照这样的方式做下去，根据上述计算猜想第四个矩形的面积为 ；第
个矩形的面积为 ．
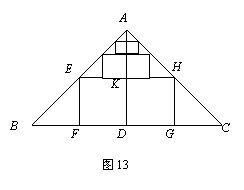
已知：如图13，等腰△ABC中，底边BC=12，高AD=6．
（1）在△ABC内作矩形EFGH，使F、G在BC上，E、H分别在AB、AC上，且长是宽的2倍．求矩形EFGH的面积．
（2）在（1）的基础上，再作第二个矩形，使其两个顶点在EH上，另外两个顶点分别在AB、AC上，且长是宽的2倍．则第二个矩形的面积为 ；
（3）在（2）的基础上，再作第三个矩形，使其两个顶点在第二个矩形的边上，另外两个顶点分别在AB、AC上，且长是宽的2倍．则第三个矩形的面积为 ；
（4）按照这样的方式做下去，根据上述计算猜想第四个矩形的面积为 ；第
个矩形的面积为 ．
个矩形的面积为 ．
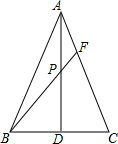已知：如图所示，在△ABC中，AB=AC，AD是BC边上的高，P是AD的中点，延长BP交AC于点F．