摘要：如图.直线与反比例函数的图像.在第一象限交于一点P.且.
网址：http://m.1010jiajiao.com/timu_id_672472[举报]
如图，直线y=x＋1与y轴交于A点，与反比列函数y=
(x>0)的图象交于点M，过M作MH⊥x，且tan∠AHO=
．
(1)求k的值；
(2)设点N（1，a）是反比例函数y=（x>0）图像上的点，在y轴上是否存在点P，使得PM＋PN最小，若存在，求出点P的坐标；若不存在，请说明理由．
如图，直线y=x＋1与y轴交于A点，与反比列函数y=
(x>0)的图象交于点M，过M作MH⊥x，且tan∠AHO=
．
(1)求k的值；
(2)设点N（1，a）是反比例函数y=（x>0）图像上的点，在y轴上是否存在点P，使得PM＋PN最小，若存在，求出点P的坐标；若不存在，请说明理由．
(x>0)的图象交于点M，过M作MH⊥x，且tan∠AHO=．(1)求k的值；
(2)设点N（1，a）是反比例函数y=
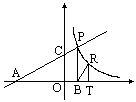
（x>0）图像上的点，在y轴上是否存在点P，使得PM＋PN最小，若存在，求出点P的坐标；若不存在，请说明理由．如图，直线y＝
x＋2分别交x、y轴于A、C，点P是该直线上在第一象限内的一点，PB⊥x轴，B为垂足，S△ABP＝9．(1)求点P的坐标；(2)设点R与点P在同一反比例函数的同一支图像上，且点正在直线PB的右侧，作RT⊥x轴，T为垂足，当△BRT与△AOC相似时，求点R的坐标．
查看习题详情和答案>>
），B（2，0）直线AB与反比例函数y=
的图像交与点C和点D（-1，a）
（x＞0，k是常数）的图像经过A（1，4），B（m，n），其中m＞1，过点A作x轴的垂线，垂足为C，过点B作y轴的垂线，垂足为D， AC与BD相交于点E，连结AD。