摘要:分式.则的计算结果为
网址:http://m.1010jiajiao.com/timu_id_672428[举报]
在计算S=1+4+7+10+13+16+19+22+25+28时,我们发现,从第一个数开始,后面的每个数与它的前面一个数的差都是一个相等的常数,具有这种规律
的一列数,除了直接相加外,还可以用公式![]() 计算, 其中n表示这一列数的个
计算, 其中n表示这一列数的个
数,![]() 表示第一个数,
表示第一个数,![]() 表示最后一个数.
表示最后一个数.
即:S=1+4+7+10+13+16+19+22+25+28=![]() =145.
=145.
用上面的知识解答下面问题:
某公司对外招商承包一分公司,符合条件的两企业A、B分别拟定上缴利润方案如下:
A:每年结算一次上缴利润,第一年上缴1.5万元,以后每年比前一年增加1万元;
B:每半年结算一次上缴利润,第一个半年上缴0.3万元,以后每半年比前半年增加0.3万元;
(![]() 1)如果承包期限2年,则A企业上缴利润的总金额为 万元,B企业上缴利润的
1)如果承包期限2年,则A企业上缴利润的总金额为 万元,B企业上缴利润的
总金额为 万元;
(2)如果承包期限为n年,分别求两企业A、B上缴利润的金额;(用含n的代数式表示)
(3)如果承包期限n=20时,那么哪个企业上缴利润的金额比较多?
查看习题详情和答案>>
(1)计算:2-1+20070+
+tan45°;
(2)化简求值:(1+
)•(x2-1),其中x=
.
(3)在数学上,对于两个数p和q有三种平均数,即算术平均数A、几何平均数G、调和平均数H,其中A=
,G=
.而调和平均数中的“调和”二字来自于音乐,毕达哥拉斯学派通过研究发现,如果三根琴弦的长度p=10,H=12,q=15满足
-
=
-
,再把它们绷得一样紧,并用同样的力弹拨,它们将会分别发出很调和的乐声.我们称p、H、q为一组调和数,而把H称为p和q的调和平均数.
①若p=2,q=6,则A= ,G= .
②根据上述关系,用p、q的代数式表示出它们的调和平均数H;并根据你所得到的结论,再写出一组调和数. 查看习题详情和答案>>
| 1 | ||
|
(2)化简求值:(1+
| 1 |
| x-1 |
| 1 |
| 3 |
(3)在数学上,对于两个数p和q有三种平均数,即算术平均数A、几何平均数G、调和平均数H,其中A=
| p+q |
| 2 |
| pq |
| 1 |
| 10 |
| 1 |
| 12 |
| 1 |
| 12 |
| 1 |
| 15 |
①若p=2,q=6,则A=
②根据上述关系,用p、q的代数式表示出它们的调和平均数H;并根据你所得到的结论,再写出一组调和数. 查看习题详情和答案>>
(1)计算:2-1+20070+ +tan45°;
+tan45°;
(2)化简求值: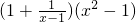 ,其中x=
,其中x= .
.
(3)在数学上,对于两个数p和q有三种平均数,即算术平均数A、几何平均数G、调和平均数H,其中A=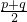 ,G=
,G=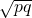 .而调和平均数中的“调和”二字来自于音乐,毕达哥拉斯学派通过研究发现,如果三根琴弦的长度p=10,H=12,q=15满足
.而调和平均数中的“调和”二字来自于音乐,毕达哥拉斯学派通过研究发现,如果三根琴弦的长度p=10,H=12,q=15满足 -
- =
= -
- ,再把它们绷得一样紧,并用同样的力弹拨,它们将会分别发出很调和的乐声.我们称p、H、q为一组调和数,而把H称为p和q的调和平均数.
,再把它们绷得一样紧,并用同样的力弹拨,它们将会分别发出很调和的乐声.我们称p、H、q为一组调和数,而把H称为p和q的调和平均数.
①若p=2,q=6,则A=______,G=______.
②根据上述关系,用p、q的代数式表示出它们的调和平均数H;并根据你所得到的结论,再写出一组调和数.
查看习题详情和答案>>
(1)计算:2-1+20070+
+tan45°;
(2)化简求值:(1+
)•(x2-1),其中x=
.
(3)在数学上,对于两个数p和q有三种平均数,即算术平均数A、几何平均数G、调和平均数H,其中A=
,G=
.而调和平均数中的“调和”二字来自于音乐,毕达哥拉斯学派通过研究发现,如果三根琴弦的长度p=10,H=12,q=15满足
-
=
-
,再把它们绷得一样紧,并用同样的力弹拨,它们将会分别发出很调和的乐声.我们称p、H、q为一组调和数,而把H称为p和q的调和平均数.
①若p=2,q=6,则A=______,G=______.
②根据上述关系,用p、q的代数式表示出它们的调和平均数H;并根据你所得到的结论,再写出一组调和数.
查看习题详情和答案>>
| 1 | ||
|
(2)化简求值:(1+
| 1 |
| x-1 |
| 1 |
| 3 |
(3)在数学上,对于两个数p和q有三种平均数,即算术平均数A、几何平均数G、调和平均数H,其中A=
| p+q |
| 2 |
| pq |
| 1 |
| 10 |
| 1 |
| 12 |
| 1 |
| 12 |
| 1 |
| 15 |
①若p=2,q=6,则A=______,G=______.
②根据上述关系,用p、q的代数式表示出它们的调和平均数H;并根据你所得到的结论,再写出一组调和数.
如图,OB、OC分别为∠ABC,∠ACB的平分线,∠BOC随着∠A的变化而变化.为探究∠A和∠BOC的关系,现采取如下两种方案,在变化过程中,设∠A为x°,∠BOC为y°.
方案甲:用量角器量出∠A、∠BOC的不断变化时的具体数据,并列表如下: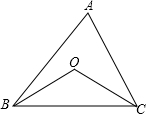
建立直角坐标系,并描点、连线,猜测y与x之间的函数关系,求出y与x的函数关系式.
方案乙:利用角平分线的性质及三角形内角和为180°的性质,直接进行计算,求出y与x之间的函数关系.
(1)若x=60°,则y= .(请直接写 出结果)
出结果)
(2)请采用方案甲或方案乙中的一种进行解答,得到∠A与∠BOC之间的关系. 查看习题详情和答案>>
方案甲:用量角器量出∠A、∠BOC的不断变化时的具体数据,并列表如下:

| x | 10 | 20 | 30 | 40 | … |
| y | 95 | 100 | 105 | 110 | … |
方案乙:利用角平分线的性质及三角形内角和为180°的性质,直接进行计算,求出y与x之间的函数关系.
(1)若x=60°,则y=
 出结果)
出结果)(2)请采用方案甲或方案乙中的一种进行解答,得到∠A与∠BOC之间的关系. 查看习题详情和答案>>