摘要：探究二: 在等腰Rt△ABC中．请你找出其它的裁剪线.把分割成的两部分拼出不同类型的特殊四边形． (1)试一试――你能拼得所有不同类型的特殊四边形有 , 他们的裁剪线分别是 , (2)画一画――请在图③中画出一个你拼得的特殊四边形示意图．
网址：http://m.1010jiajiao.com/timu_id_671721[举报]
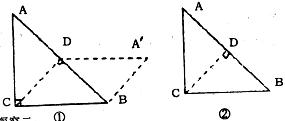
把一个等腰Rt△ABC；沿斜边上的离线CD(裁剪线)剪一刀，从这一个三角形中裁下一部分，与剩下部分能拼成一个平行四边形
见示意图①．以下探究过程中有画图要求的，工具不限，不必写画法和证明．
探究一：
(1)想一想――判断四边形是平行四边形的依据．
(2)做一做――按上述的裁剪方法，请你拼一个与图①位置或形状不同的平行四边形，并在图②中画出示意图．
探究二：
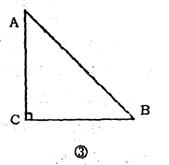
在等腰Rt△ABC中．请你找出其它的裁剪线，把分割成的两部分拼出不同类型的特殊四边形．
(1)试一试――你能拼得所有不同类型的特殊四边形有_________；
他们的裁剪线分别是_______；
(2)画一画――请在图③中画出一个你拼得的特殊四边形示意图．
查看习题详情和答案>>（2011•裕华区二模）如图①，将两个等腰直角三角形叠放在一起，使上面三角板的一个锐角顶点与下面三角板的直角顶点重合，并将上面的三角板绕着这个顶点逆时针旋转，在旋转过程中，当下面三角板的斜边被分成三条线段时，我们来研究这三条线段之间的关系．
（1）实验与操作：
如图②，如果上面三角板的一条直角边旋转到CM的位置时，它的斜边恰好旋转到CN的位置，请在网格中分别画出以AM、MN和NB为边长的正方形，观察这三个正方形的面积之间的关系；
（2）猜想与探究：
如图③，在Rt△ABC中，BC=AC，∠ACB=90°，M、N是AB边上的点，∠MCN=45°，作DA⊥AB于点A，截取DA=NB，并连接DC、DM．
我们来证明线段CD与线段CN相等．
∵∠CAB=∠CBA=45°，又DA⊥AB于点A，
∴∠DAC=45°，∴∠DAC=∠CBA，
又∵DA=NB，BC=AC，
∴△CAD≌△CBN．
∴CD=CN．
请你继续解答：
①线段MD与线段MN相等吗？为什么？
②线段AM、MN、NB有怎样的数量关系，为什么？
（3）拓广与运用：
如图④，已知线段AB上任意一点M（AM＜MB），是否总能在线段MB上找到一点N，使得分别以AM与BN为边长的正方形的面积的和等于以MN为边长的正方形的面积？若能，请在图④中画出点N的位置，并简要说明作法；若不能，请说明理由．
查看习题详情和答案>>
（1）实验与操作：
如图②，如果上面三角板的一条直角边旋转到CM的位置时，它的斜边恰好旋转到CN的位置，请在网格中分别画出以AM、MN和NB为边长的正方形，观察这三个正方形的面积之间的关系；
（2）猜想与探究：
如图③，在Rt△ABC中，BC=AC，∠ACB=90°，M、N是AB边上的点，∠MCN=45°，作DA⊥AB于点A，截取DA=NB，并连接DC、DM．
我们来证明线段CD与线段CN相等．
∵∠CAB=∠CBA=45°，又DA⊥AB于点A，
∴∠DAC=45°，∴∠DAC=∠CBA，
又∵DA=NB，BC=AC，
∴△CAD≌△CBN．
∴CD=CN．
请你继续解答：
①线段MD与线段MN相等吗？为什么？
②线段AM、MN、NB有怎样的数量关系，为什么？
（3）拓广与运用：
如图④，已知线段AB上任意一点M（AM＜MB），是否总能在线段MB上找到一点N，使得分别以AM与BN为边长的正方形的面积的和等于以MN为边长的正方形的面积？若能，请在图④中画出点N的位置，并简要说明作法；若不能，请说明理由．