摘要：(2)如图②.已知是线段BC的中点.现沿着由B到的方向.将△DBC平移到的位置.连结..得到四边形是什么特殊的四边形?说明你的理由．
网址：http://m.1010jiajiao.com/timu_id_671714[举报]
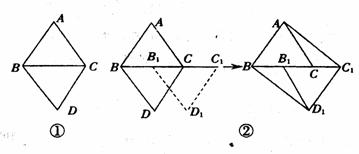
如图①，已知等边△ABC和等边△DBC有公共的底边BC
(1)以图①中的某个点为旋转中心，旋转△ABC和△DBC重合则旋转中心为________(写出所有满足条件的点)；
(2)如图②，已知
是线段BC的中点，现沿着由B到的方向，将△DBC平移到
的位置，连结
，
，得到四边形
是什么特殊的四边形?说明你的理由．
(3)在四边形中有_________对全等三角形?请你选出其中一对进行证明．
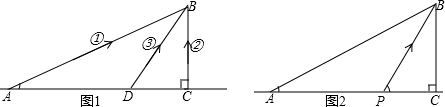
如图，海事救援指挥中心A接到海上SOS呼救：一艘渔船B在海上碰到暗礁，船体漏水下沉，5名船员需要援救．经测量渔船B到海岸最近的点C的距离BC=20km，∠BAC=22°37′，指挥中心立即制定三种救援方案（如图1）：
①派一艘冲锋舟直接从A开往B；②先用汽车将冲锋舟沿海岸线送到点C，然后再派冲锋舟前往B；③先用汽车将冲锋舟沿海岸线送到距指挥中心33km的点D，然后再派冲锋舟前往B．
已知冲锋舟在海上航行的速度为60km/h，汽车在海岸线上行驶的速度为90km/h．
（sin22°37′=
，cos22°37′=
，tan22°37′=
）
（1）通过计算比较，这三种方案中，哪种方案较好（汽车装卸冲锋舟的时间忽略不计）？
（2）事后，细心的小明发现，上面的三种方案都不是最佳方案，最佳方案应是：先用汽车将冲锋舟沿海岸线送到点P处，点P满足cos∠BPC=
（冲锋舟与汽车速度的比），然后再派冲锋舟前往B（如图2）．请你说明理由！
如果你反复探索没有解决问题，可以选取①、②、③两种研究方法：
方案①：在线段上AP任取一点M；然后用转化的思想，从几何的角度说明汽车行AM加上冲锋舟行BM的时间比车行AP加上冲锋舟行BP的时间要长．
方案②：在线段上AP任取一点M；设AM=x；然后用含有x的代数式表示出所用时间t；
方案③：利用现有数据，根据cos∠BPC=
计算出汽车行AP加上冲锋舟行BP的时间．
查看习题详情和答案>>
①派一艘冲锋舟直接从A开往B；②先用汽车将冲锋舟沿海岸线送到点C，然后再派冲锋舟前往B；③先用汽车将冲锋舟沿海岸线送到距指挥中心33km的点D，然后再派冲锋舟前往B．
已知冲锋舟在海上航行的速度为60km/h，汽车在海岸线上行驶的速度为90km/h．
（sin22°37′=
| 5 |
| 13 |
| 12 |
| 13 |
| 5 |
| 12 |
（1）通过计算比较，这三种方案中，哪种方案较好（汽车装卸冲锋舟的时间忽略不计）？
（2）事后，细心的小明发现，上面的三种方案都不是最佳方案，最佳方案应是：先用汽车将冲锋舟沿海岸线送到点P处，点P满足cos∠BPC=
| 2 |
| 3 |
如果你反复探索没有解决问题，可以选取①、②、③两种研究方法：
方案①：在线段上AP任取一点M；然后用转化的思想，从几何的角度说明汽车行AM加上冲锋舟行BM的时间比车行AP加上冲锋舟行BP的时间要长．
方案②：在线段上AP任取一点M；设AM=x；然后用含有x的代数式表示出所用时间t；
方案③：利用现有数据，根据cos∠BPC=
| 2 |
| 3 |
查看习题详情和答案>>
如图，矩形ABCD中，AB="10" cm，BC="6" cm．现有两个动点P，Q分别从A，B同时出发，点P在线段AB上沿AB方向作匀速运动，点Q在线段BC上沿BC方向作匀速运动，已知点P的运动速度为1 cm/s，运动时间为t s．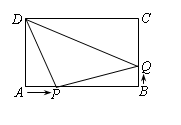
（1）设点Q的运动速度为
cm/s．
①当△DPQ的面积最小时，求t的值；
②当△DAP∽△QBP相似时，求t的值．
（2）设点Q的运动速度为a cm/s，问是否存在a的值，使得△DAP与△PBQ和△QCD这两个三角形都相似？若存在，请求出a的值；若不存在，请说明理由．
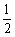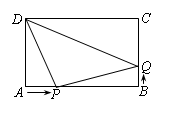
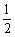cm/s．
cm/s．