题目内容
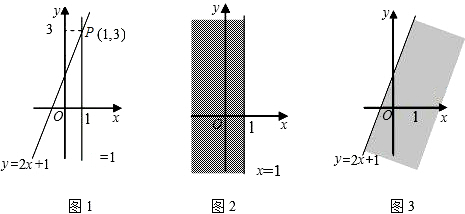
我们知道,在数轴上,x=1表示一个点,而在平面直角坐标系中,x=1表示一条直线;我们还知道,以二元一次方程2x-y+1=0的所有解为坐标的点组成的图形就是一次函数y=2x+1的图象,它也是一条直线,如图1.观察图1可以得出:直线x=1与直线y=2x+1的交点P的坐标(1,3)就是
方程组
|
|
在直角坐标系中,x≤1表示一个平面区域,即直线x=1以及它左侧的部分,如图②;y≤2x+1也表示一个平面区域,即直线y=2x+1以及它下方的部分,如图3;
那么,
|

回答下列问题:
(1)在下面的直角坐标系中,用作图象的方法求出方程组
|
(2)在右面的直角坐标系中用阴影表示,
|
分析:(1)求的方程组的解实际是一次函数x=2和y=
x+3的交点坐标,可先画出这两个一次函数,得到交点后,交点的横坐标就是方程组的x的值,纵坐标就是方程组的y的值.
(2)方程组中x≤2实际是直线x=2下方的区域,那么同理可先作出各函数的图形,然后根据不等式符号的不同,来得出不同的区域,由函数所得区域的重叠部分就是围成的区域.
| 3 |
| 2 |
(2)方程组中x≤2实际是直线x=2下方的区域,那么同理可先作出各函数的图形,然后根据不等式符号的不同,来得出不同的区域,由函数所得区域的重叠部分就是围成的区域.
解答: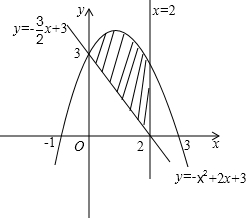 解:(1)在坐标系中分别作出直线x=2和直线y=-
解:(1)在坐标系中分别作出直线x=2和直线y=-
x+3,
这两条直线的交点是(2,0).
则x=2,y=0就是方程组
的解.
(2)在(1)问的前提下作出y=-x2+2x+3的图象,
则
所围成的区域如图阴影所示.
 解:(1)在坐标系中分别作出直线x=2和直线y=-
解:(1)在坐标系中分别作出直线x=2和直线y=-| 3 |
| 2 |
这两条直线的交点是(2,0).
则x=2,y=0就是方程组
|
(2)在(1)问的前提下作出y=-x2+2x+3的图象,
则
|
点评:本题要求利用图象求解各问题,先画函数图象,根据图象观察,得出结论.认真体会一次函数与一元一次方程及一元一次不等式之间的内在联系.

练习册系列答案
相关题目

 右运动,当点A到达何位置时,小车被阴影部分挡住的面积最大?
右运动,当点A到达何位置时,小车被阴影部分挡住的面积最大?