摘要：③直接利用②中的规律计算的结果.

网址：http://m.1010jiajiao.com/timu_id_670816[举报]

我国古籍《周髀算经》中早有记载“勾三股四弦五”，下面我们来探究两类特殊的勾股数．
（1）通过观察完成下面两个表格中的空格（以下a、b、c为Rt△ABC的三边，且a＜b＜c）：

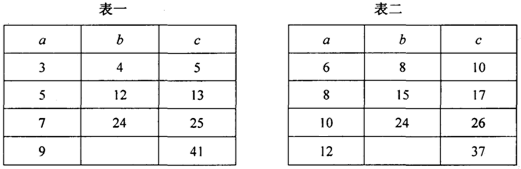
（2）我们发现，表一中a为大于l的奇数，此时b、c的数量关系是
b+1=c
b+1=c
；表二中a为大于4的偶数，此时b、c的数量关系是
b+2=c
b+2=c
；
（3）一般地，对于表一，用含a的代数式表示b=
a2-1
2
a2-1
2
；对于表二，用含a的代数式表示b=
a2
4
-1
a2
4
-1
；
（4）我们还发现，表一中的三边长“3，4，5”与表二中的“6，8，10”成倍数关系，表一中的“5，l2，13”与表二中的“10，24，26”恰好也成倍数关系…．请直接利用这一规律计算：在Rt△ABC中，当a=
3
5
，b=
4
5
时，斜边c的值．
 查看习题详情和答案>>

我国古籍《周髀算经》中早有记载“勾三股四弦五”，下面我们来探究两类特殊的勾股数．
（1）通过观察完成下面两个表格中的空格（以下a、b、c为Rt△ABC的三边，且a＜b＜c）：
作业宝
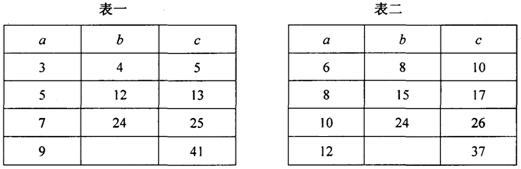
（2）我们发现，表一中a为大于l的奇数，此时b、c的数量关系是______；表二中a为大于4的偶数，此时b、c的数量关系是______；
（3）一般地，对于表一，用含a的代数式表示b=______；对于表二，用含a的代数式表示b=______；
（4）我们还发现，表一中的三边长“3，4，5”与表二中的“6，8，10”成倍数关系，表一中的“5，l2，13”与表二中的“10，24，26”恰好也成倍数关系…．请直接利用这一规律计算：在Rt△ABC中，当a=数学公式，b=数学公式时，斜边c的值．

 查看习题详情和答案>>
观察下列各式，通过分母有理化，把不是最简二次根式的化成最简二次根式．
1
2
+1
=
1×(
2
-1)
(
2
+1)(
2
-1)
=
2
-1
2-1
=
2
-1
1
3
+
2
=
1×(
3
-
2
)
(
3
+
2
)(
3
-
2
)
=
3
-
2
3-2
=
3
-
2

同理可得：
1
4
+
3
=
4
-
3

从计算结果中找出规律，并利用这一规律计算：
1
2
+1
+
1
3
+
2
+
1
4
+
3
+…+
1
2013
+
2012
（
2013
+1）
 查看习题详情和答案>>
阅读下面问题：
1
2
+1
=
2
-1，
1
3
+
2
=
3
-
2
，
1
4
+
3
=
4
-
3
，
1
5
+
4
=
5
-
4
，…
从计算结果中找出规律，再利用这一规律计算下列式子的值：
(
1
2
+1
+
1
3
+
2
+
1
4
+
3
+…+
1
2002
+
2001
)(
2002
+1)． 查看习题详情和答案>>
观察下列分母有理化的计算：
1
2
+1
=
2
-1，
1
3
+
2
=
3
-
2
，
1
4
-
3
=
4
-
3
，
1
5
+
4
=
5
-
4
…在计算结果中找出规律，用含字母n（n表示大于0的自然数）表示；再利用这一规律计算下列式子的值：（
1
2
+
1
+
1
3
+
2
+
1
4
+
3
+…+
1
2014
+
2013
）（
2014
+1） 的值．
 查看习题详情和答案>>

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网