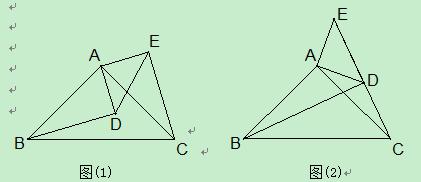
摘要:(1)连结 (2)猜想 (3)证明你的猜想:
网址:http://m.1010jiajiao.com/timu_id_669315[举报]
推理证明:如图1,在正方形ABCD和正方形CGFE中,连结DE、BG,设△DCE的面积为S1,△BCG的面积为S2,求证:S1=S2.
猜想论证:如图2,将矩形ABCD绕点C按顺时针方向旋转后得到矩形FECG,连结DE、BG,设△DCE的面积为S1,△BCG的面积为S2,猜想S1、S2的数量关系,并加以证明.
拓展探究:如图3,在△ABC中,AB=AC=10cm,∠B=30°,把△ABC沿AC翻折到△ACE,过点A作AD∥CE交BC于点D,在线段CE上存在点P,使△ABP的面积等于△ACD的面积,请你直接写出CP的长.

查看习题详情和答案>>
猜想论证:如图2,将矩形ABCD绕点C按顺时针方向旋转后得到矩形FECG,连结DE、BG,设△DCE的面积为S1,△BCG的面积为S2,猜想S1、S2的数量关系,并加以证明.
拓展探究:如图3,在△ABC中,AB=AC=10cm,∠B=30°,把△ABC沿AC翻折到△ACE,过点A作AD∥CE交BC于点D,在线段CE上存在点P,使△ABP的面积等于△ACD的面积,请你直接写出CP的长.

【图形变换的探究与猜想】
从特殊到一般,从全等到相似;求证线段的数量关系或位置关系.关键是第一问的全等的证明,发现全等的三角形,一般是利用ASA完成证明,从而得到需要证明的相似三角形(利用两边对应成比例且夹角相等).
例:正方形ABCD,E为直线AB上任意一点,DF⊥DE交直线BC于点F,直线EF、AC交于点H,连接DH.
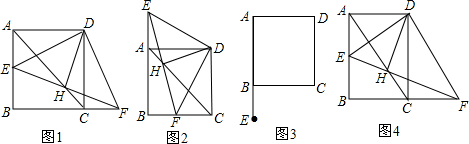
(1)①如图1,当点E在边AB上时,判断线段DH与线段EF之间的数量关系和位置关系;
②如图2,当点E在边AB的反向延长线上时,判断线段DH与线段EF之间的数量关系和位置关系;写出你的结论并从①、②中任选一个证明;
(2)如图3,若点E在AB边的延长线上,其它条件不变,完成图3,判断线段DH与线段EF之间的数量关系和位置关系,直接写出你的结论,不需要证明;
(3)如图4,若将图1中的正方形ABCD改为矩形ABCD为正方形,且AB=kAD,其它条件不变,判断线段DH与线段EF之间的数量关系和位置关系,直接写出结论,不需要证明.
查看习题详情和答案>>
从特殊到一般,从全等到相似;求证线段的数量关系或位置关系.关键是第一问的全等的证明,发现全等的三角形,一般是利用ASA完成证明,从而得到需要证明的相似三角形(利用两边对应成比例且夹角相等).
例:正方形ABCD,E为直线AB上任意一点,DF⊥DE交直线BC于点F,直线EF、AC交于点H,连接DH.

(1)①如图1,当点E在边AB上时,判断线段DH与线段EF之间的数量关系和位置关系;
②如图2,当点E在边AB的反向延长线上时,判断线段DH与线段EF之间的数量关系和位置关系;写出你的结论并从①、②中任选一个证明;
(2)如图3,若点E在AB边的延长线上,其它条件不变,完成图3,判断线段DH与线段EF之间的数量关系和位置关系,直接写出你的结论,不需要证明;
(3)如图4,若将图1中的正方形ABCD改为矩形ABCD为正方形,且AB=kAD,其它条件不变,判断线段DH与线段EF之间的数量关系和位置关系,直接写出结论,不需要证明.