题目内容
【图形变换的探究与猜想】
从特殊到一般,从全等到相似;求证线段的数量关系或位置关系.关键是第一问的全等的证明,发现全等的三角形,一般是利用ASA完成证明,从而得到需要证明的相似三角形(利用两边对应成比例且夹角相等).
例:正方形ABCD,E为直线AB上任意一点,DF⊥DE交直线BC于点F,直线EF、AC交于点H,连接DH.
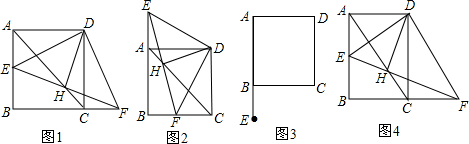
(1)①如图1,当点E在边AB上时,判断线段DH与线段EF之间的数量关系和位置关系;
②如图2,当点E在边AB的反向延长线上时,判断线段DH与线段EF之间的数量关系和位置关系;写出你的结论并从①、②中任选一个证明;
(2)如图3,若点E在AB边的延长线上,其它条件不变,完成图3,判断线段DH与线段EF之间的数量关系和位置关系,直接写出你的结论,不需要证明;
(3)如图4,若将图1中的正方形ABCD改为矩形ABCD为正方形,且AB=kAD,其它条件不变,判断线段DH与线段EF之间的数量关系和位置关系,直接写出结论,不需要证明.
从特殊到一般,从全等到相似;求证线段的数量关系或位置关系.关键是第一问的全等的证明,发现全等的三角形,一般是利用ASA完成证明,从而得到需要证明的相似三角形(利用两边对应成比例且夹角相等).
例:正方形ABCD,E为直线AB上任意一点,DF⊥DE交直线BC于点F,直线EF、AC交于点H,连接DH.

(1)①如图1,当点E在边AB上时,判断线段DH与线段EF之间的数量关系和位置关系;
②如图2,当点E在边AB的反向延长线上时,判断线段DH与线段EF之间的数量关系和位置关系;写出你的结论并从①、②中任选一个证明;
(2)如图3,若点E在AB边的延长线上,其它条件不变,完成图3,判断线段DH与线段EF之间的数量关系和位置关系,直接写出你的结论,不需要证明;
(3)如图4,若将图1中的正方形ABCD改为矩形ABCD为正方形,且AB=kAD,其它条件不变,判断线段DH与线段EF之间的数量关系和位置关系,直接写出结论,不需要证明.
分析:(1)①求出AD=DC,∠EAD=∠FCD,∠EDA=∠FDC,证△EAD≌△FCD,推出ED=DF,求出∠EDF=90°,求出∠DFE=45°=∠DCA,推出D、H、C、F四点共圆,推出∠DHF=∠DCF=90°,根据等腰三角形性质和直角三角形斜边上中线性质求出DH=
EF即可;
②求出AD=DC,∠EAD=∠FCD,∠EDA=∠FDC,证△EAD≌△FCD,推出ED=DF,求出∠EDF=90°,求出∠DFE=45°=∠DCA,推出D、H、F、C四点共圆,推出∠DHF=∠DCF=90°,根据等腰三角形性质和直角三角形斜边上中线性质求出DH=
EF即可;
(2)画出图形,证△ADE≌△CDF,推出DE=DF,求出∠EDF=90°,求出∠DFE=45°=∠DCA,推出D、H、F、C四点共圆,推出∠DHF=∠DCF=90°,根据等腰三角形性质和直角三角形斜边上中线性质求出DH=
EF即可;
(3)证△ADE∽△CDF,推出
=
=
,根据解直角三角形求出∠DFE=∠DCA,推出D、F、C、H、四点共圆,推出∠DHF=∠DCF=90°,设DE=x,DF=kx,根据勾股定理EF=
x,证△DHE∽△FDE,求出DH,即可求出答案.

| 1 |
| 2 |
②求出AD=DC,∠EAD=∠FCD,∠EDA=∠FDC,证△EAD≌△FCD,推出ED=DF,求出∠EDF=90°,求出∠DFE=45°=∠DCA,推出D、H、F、C四点共圆,推出∠DHF=∠DCF=90°,根据等腰三角形性质和直角三角形斜边上中线性质求出DH=
| 1 |
| 2 |
(2)画出图形,证△ADE≌△CDF,推出DE=DF,求出∠EDF=90°,求出∠DFE=45°=∠DCA,推出D、H、F、C四点共圆,推出∠DHF=∠DCF=90°,根据等腰三角形性质和直角三角形斜边上中线性质求出DH=
| 1 |
| 2 |
(3)证△ADE∽△CDF,推出
| DE |
| DF |
| AD |
| DC |
| 1 |
| k |
| 1+k2 |

解答:解:(1)①DH=
EF,DH⊥EF,
理由是:∵四边形ABCD是正方形,
∴AD=DC,∠DCA=45°,∠DAE=∠ADC=∠DCB=∠DCF=90°,
∵ED⊥DF,
∴∠EDF=∠ADC=90°,
∴∠ADC-∠EDC=∠EDF-∠EDC,
即∠ADE=∠CDF,
在△EAD和△FCD中
∴△EAD≌△FCD(ASA),
∴DE=DF,
∵∠EDF=90°,
∴∠DEF=∠DFE=45°=∠ACD,
∴D、H、C、F四点共圆,
∴∠DHF=∠DCF=90°,
∴DH⊥EF,
∵DE=DF,
∴EH=FH,
∵∠EDF=90°,
∴DH=
EF.
②DH=
EF,DH⊥EF,
证明过程和①类似.
(2) DH=
DH=
EF,DH⊥EF.证明过程和①类似.
(3)DH⊥EF,DH=
EF,
理由是:∵由①知,∠ADE=∠FDC,∠DAE=∠DCF,
∴△ADE∽△CDF,
∴
=
,
∵AB=DCkAD,
∴DE=kDF,
设DE=x,DF=kx,
在Rt△EDF中,由勾股定理得:EF=
=
x,
∵在Rt△CDA中,tan∠DCA=
=
,在Rt△DEF中,tan∠DFE=
=
=
,
∴∠DCA=∠DFE,
∴∠DHF=∠DCF=90°,
∴DH⊥EF,
∴∠DHE=∠EDF,
∵∠DEF=∠DEH,
∴△DHE∽△FDE,
∴
=
,
∴DH=
•x=
,
∵EF=
x,
∴DH=
EF.
| 1 |
| 2 |
理由是:∵四边形ABCD是正方形,
∴AD=DC,∠DCA=45°,∠DAE=∠ADC=∠DCB=∠DCF=90°,
∵ED⊥DF,
∴∠EDF=∠ADC=90°,
∴∠ADC-∠EDC=∠EDF-∠EDC,
即∠ADE=∠CDF,
在△EAD和△FCD中
|
∴△EAD≌△FCD(ASA),
∴DE=DF,
∵∠EDF=90°,

∴∠DEF=∠DFE=45°=∠ACD,
∴D、H、C、F四点共圆,
∴∠DHF=∠DCF=90°,
∴DH⊥EF,
∵DE=DF,
∴EH=FH,
∵∠EDF=90°,
∴DH=
| 1 |
| 2 |
②DH=
| 1 |
| 2 |
证明过程和①类似.
(2)
 DH=
DH=| 1 |
| 2 |
(3)DH⊥EF,DH=
| 1 |
| 1+k2 |
理由是:∵由①知,∠ADE=∠FDC,∠DAE=∠DCF,
∴△ADE∽△CDF,
∴
| AD |
| DC |
| DE |
| DF |
∵AB=DCkAD,
∴DE=kDF,
设DE=x,DF=kx,
在Rt△EDF中,由勾股定理得:EF=
| DE2+DF2 |
| 1+k2 |
∵在Rt△CDA中,tan∠DCA=
| AD |
| DC |
| 1 |
| k |
| DE |
| DF |
| AD |
| DC |
| 1 |
| k |
∴∠DCA=∠DFE,
∴∠DHF=∠DCF=90°,
∴DH⊥EF,
∴∠DHE=∠EDF,
∵∠DEF=∠DEH,
∴△DHE∽△FDE,
∴
| DH |
| DE |
| DE |
| EF |
∴DH=
| x | ||
|
| x | ||
|
∵EF=
| 1+k2 |
∴DH=
| 1 |
| 1+k2 |
点评:本题考查了全等三角形的性质和判定,相似三角形的性质和判定,等腰三角形的性质和判定,直角三角形斜边上中线的性质,解直角三角形,勾股定理等知识点的应用,主要考查学生的推理能力,难度偏大.

练习册系列答案
相关题目