摘要: 点N.先向左平移3个单位.又向上平移2个单位得到点M.则点M的坐标为 A.(6.O) B. C. D.(O.O)
网址:http://m.1010jiajiao.com/timu_id_667926[举报]
我们知道,对于二次函数y=a(x+m)2+k的图象,可由函数y=ax2的图象进行向左或向右平移一次、再向上或向下移一次平移得到,我们称函数y=ax2为“基本函数”,而称由它平移得到的二次函数y=a(x+m)2+k为“基本函数”y=ax2的“朋友函数”.左右、上下平移的路径称为朋友路径,对应点之间的线段距离
称为朋友距离.
由此,我们所学的函数:二次函数y=ax2,函数y=kx和反比例函数y=
都可以作为“基本函数”,并进行向左或向右平移一次、再向上或向下平移一次得到相应的“朋友函数”.
如一次函数y=2x-5是基本函数y=2x的朋友函数,由y=2x-5=2(x-1)-3朋友路径可以是向右平移1个单位,再向下平移3个单位,朋友距离=
=
.
(1)探究一:小明同学经过思考后,为函数y=2x-5又找到了一条朋友路径为由基本函数y=2x先向 ,再向下平移7单位,相应的朋友距离为 .
(2)探究二:已知函数y=x2-6x+5,求它的基本函数,朋友路径,和相应的朋友距离.
(3)探究三:为函数y=
和它的基本函数y=
,找到朋友路径,并求相应的朋友距离.
查看习题详情和答案>>
| m2+k2 |
由此,我们所学的函数:二次函数y=ax2,函数y=kx和反比例函数y=
| k |
| x |
如一次函数y=2x-5是基本函数y=2x的朋友函数,由y=2x-5=2(x-1)-3朋友路径可以是向右平移1个单位,再向下平移3个单位,朋友距离=
| 12+32 |
| 10 |
(1)探究一:小明同学经过思考后,为函数y=2x-5又找到了一条朋友路径为由基本函数y=2x先向
(2)探究二:已知函数y=x2-6x+5,求它的基本函数,朋友路径,和相应的朋友距离.
(3)探究三:为函数y=
| 3x+4 |
| x+1 |
| 1 |
| x |
我们知道,对于二次函数y=a(x+m)2+k的图象,可由函数y=ax2的图象进行向左或向右平移一次、再向上或向下移一次平移得到,我们称函数y=ax2为“基本函数”,而称由它平移得到的二次函数y=a(x+m)2+k为“基本函数”y=ax2的“朋友函数”.左右、上下平移的路径称为朋友路径,对应点之间的线段距离
称为朋友距离.
由此,我们所学的函数:二次函数y=ax2,函数y=kx和反比例函数y=
都可以作为“基本函数”,并进行向左或向右平移一次、再向上或向下平移一次得到相应的“朋友函数”.
如一次函数y=2x-5是基本函数y=2x的朋友函数,由y=2x-5=2(x-1)-3朋友路径可以是向右平移1个单位,再向下平移3个单位,朋友距离=
=
.
(1)探究一:小明同学经过思考后,为函数y=2x-5又找到了一条朋友路径为由基本函数y=2x先向______,再向下平移7单位,相应的朋友距离为______.
(2)探究二:已知函数y=x2-6x+5,求它的基本函数,朋友路径,和相应的朋友距离.
(3)探究三:为函数y=
和它的基本函数y=
,找到朋友路径,并求相应的朋友距离.
查看习题详情和答案>>
| m2+k2 |
由此,我们所学的函数:二次函数y=ax2,函数y=kx和反比例函数y=
| k |
| x |
如一次函数y=2x-5是基本函数y=2x的朋友函数,由y=2x-5=2(x-1)-3朋友路径可以是向右平移1个单位,再向下平移3个单位,朋友距离=
| 12+32 |
| 10 |
(1)探究一:小明同学经过思考后,为函数y=2x-5又找到了一条朋友路径为由基本函数y=2x先向______,再向下平移7单位,相应的朋友距离为______.
(2)探究二:已知函数y=x2-6x+5,求它的基本函数,朋友路径,和相应的朋友距离.
(3)探究三:为函数y=
| 3x+4 |
| x+1 |
| 1 |
| x |
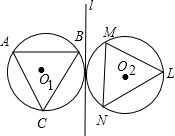
 19、如图,关于直线l对称的两个圆的半径都为1,等边三角形ABC,LMN的顶点分别在两圆上,AB⊥l,MN∥l,将l左侧的图形进行平移、旋转或翻折变换(以下所述“变换”均值这3种变换之一),可以与l右侧的图形重合.
19、如图,关于直线l对称的两个圆的半径都为1,等边三角形ABC,LMN的顶点分别在两圆上,AB⊥l,MN∥l,将l左侧的图形进行平移、旋转或翻折变换(以下所述“变换”均值这3种变换之一),可以与l右侧的图形重合.(1)通过两次变换,不难实现上述重合的目的.例如,将l左侧图先绕圆心O1,按逆时针方向旋转
30°
度,再沿l翻折,就可与右侧的图形重合;又如,将l左侧图形先向右平移2个单位,再绕圆心按顺时针方向旋转30°
度,就与右侧图形重合;(2)能否将l左侧图形只进行一次变换,就可使它与l右侧图形重合?如果能,请说明变换过程;如果不能,请你设计一种“将l左侧图形先沿着过点O1的某直线翻折,再向右适当平移”(两次变换)即可与右侧图形重合的方案.(画出该直线并予以说明)
如图,关于直线l对称的两个圆的半径都为1,等边三角形ABC,LMN的顶点分别在两圆上,AB⊥l,MN∥l,将l左侧的图形进行平移、旋转或翻折变换(以下所述“变换”均值这3种变换之一),可以与l右侧的图形重合.
(1)通过两次变换,不难实现上述重合的目的.例如,将l左侧图先绕圆心O1,按逆时针方向旋转______度,再沿l翻折,就可与右侧的图形重合;又如,将l左侧图形先向右平移2个单位,再绕圆心按顺时针方向旋转______度,就与右侧图形重合;
(2)能否将l左侧图形只进行一次变换,就可使它与l右侧图形重合?如果能,请说明变换过程;如果不能,请你设计一种“将l左侧图形先沿着过点O1的某直线翻折,再向右适当平移”(两次变换)即可与右侧图形重合的方案.(画出该直线并予以说明)
查看习题详情和答案>>
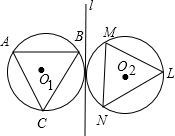
如图,关于直线l对称的两个圆的半径都为1,等边三角形ABC,LMN的顶点分别在两圆上,AB⊥l,MN∥l,将l左侧的图形进行平移、旋转或翻折变换(以下所述“变换”均值这3种变换之一),可以与l右侧的图形重合.
(1)通过两次变换,不难实现上述重合的目的.例如,将l左侧图先绕圆心O1,按逆时针方向旋转______度,再沿l翻折,就可与右侧的图形重合;又如,将l左侧图形先向右平移2个单位,再绕圆心按顺时针方向旋转______度,就与右侧图形重合;
(2)能否将l左侧图形只进行一次变换,就可使它与l右侧图形重合?如果能,请说明变换过程;如果不能,请你设计一种“将l左侧图形先沿着过点O1的某直线翻折,再向右适当平移”(两次变换)即可与右侧图形重合的方案.(画出该直线并予以说明)
查看习题详情和答案>>
(1)通过两次变换,不难实现上述重合的目的.例如,将l左侧图先绕圆心O1,按逆时针方向旋转______度,再沿l翻折,就可与右侧的图形重合;又如,将l左侧图形先向右平移2个单位,再绕圆心按顺时针方向旋转______度,就与右侧图形重合;
(2)能否将l左侧图形只进行一次变换,就可使它与l右侧图形重合?如果能,请说明变换过程;如果不能,请你设计一种“将l左侧图形先沿着过点O1的某直线翻折,再向右适当平移”(两次变换)即可与右侧图形重合的方案.(画出该直线并予以说明)
