摘要:∴ + + +--+ = 这种求和的方法叫做裂项相消法.即将和式中的每一项分拆成两项之差.使得除首项和末项外的中间所有项都相互抵消.从而达到求和目的.请利用这种方法解答下列问题:
网址:http://m.1010jiajiao.com/timu_id_667793[举报]
在计算1+4+7+10+13+16+19+22+25+28时,我们发现,从第一个数开始,后面的每个数与它的前面一个数的差都是一个相等的常数,具有这种规律的一列数,除了直接相加外,我们还可以用下列公式来求和S,S=
(其中n表示数的个数,a1表示第一个数,an表示最后一个数),所以1+4+7+10+13+16+19+22+25+28=
=145.
用上面的知识解答下面问题:
某公司对外招商承包一分公司,符合条件的两企业A、B分别拟定上缴利润方案如下:
A:每年结算一次上缴利润,第一年上缴1.5万元,以后每年比前一年增加1万元:
B:每半年结算一次上缴利润,第一个半年上缴0.3万元,以后每半年比前半年增加0.3万元.
(1)如果承包期限为4年,请你通过计算,判断哪家企业上缴利润的总金额多?
(2)如果承包期限为n年,试用n的代数式分别表示两企业上缴利润的总金额.(单位:万元)
查看习题详情和答案>>
| n(a1+an) |
| 2 |
| 10×(1+28) |
| 2 |
用上面的知识解答下面问题:
某公司对外招商承包一分公司,符合条件的两企业A、B分别拟定上缴利润方案如下:
A:每年结算一次上缴利润,第一年上缴1.5万元,以后每年比前一年增加1万元:
B:每半年结算一次上缴利润,第一个半年上缴0.3万元,以后每半年比前半年增加0.3万元.
(1)如果承包期限为4年,请你通过计算,判断哪家企业上缴利润的总金额多?
(2)如果承包期限为n年,试用n的代数式分别表示两企业上缴利润的总金额.(单位:万元)
在计算l+4+7+10+13+16+19+22+25+28时,我们发现,从第一个数开始,后面的每个数与它的前面一个数的差都是一个相等的常数,具有这种规律的一列数,除了直接相加外,我们还可以用下列公式来求和S,S=
(其中n表示数的个数,a1表示第一个数,an表示最后一个数),所以1+4+7+10+r3+16+19+22+25+28=
=145.
用上面的知识解答下面问题:某公司对外招商承包一分公司,符合条件的两企业A、B分别拟定上缴利润方案如下:
A:每年结算一次上缴利润,第一年上缴1.5万元,以后每年比前一年增加l万元;
B:每半年结算一次上缴利润,第一个半年上缴0.3万元,以后每半年比前半年增加0.3万元;
(1)如果承包期限4年,请你通过计算,判断哪家企业上缴利润的总金额多?
(2)如果承包期限为n年,试用n的代数式分别表示两企业上缴利润的总金额(单位:万元);
(3)承包期限n至少是 年,B企业上缴利润的总金额超过A企业上缴利润的总金额.
查看习题详情和答案>>
| n(a1+an) |
| 2 |
| 10×(1+28) |
| 2 |
用上面的知识解答下面问题:某公司对外招商承包一分公司,符合条件的两企业A、B分别拟定上缴利润方案如下:
A:每年结算一次上缴利润,第一年上缴1.5万元,以后每年比前一年增加l万元;
B:每半年结算一次上缴利润,第一个半年上缴0.3万元,以后每半年比前半年增加0.3万元;
(1)如果承包期限4年,请你通过计算,判断哪家企业上缴利润的总金额多?
(2)如果承包期限为n年,试用n的代数式分别表示两企业上缴利润的总金额(单位:万元);
(3)承包期限n至少是
阅读下面材料:
在计算1+4+7+10+13+16+19+22+25+28时,我们发现,从第一个数开始,以后的每个数与它的前一个数的差都是一个相同的定值,具有这种规律的一列数,求和时,除了直接相加外,我们还可以用公式S=na+
×d来计算(公式中的S表示它们的和,n表示数的个数,a表示第一个数的值,d表示这个相差的定值).那么S=1+4+7+10+13+16+19+22+25+28=10×1+
×3=145.
用上面的知识解决下列问题:
我市某乡镇具有“中国北方乔木之乡”的美称,到2000年底这个镇已有苗木2万亩,为增加农民收入,这个镇实施“苗木兴镇”战略,逐年有计划地扩种苗木.从2001年起,以后每年又比上一年多种植相同面积的苗木;从2001年起每年卖出成苗木,以后每年又比上一年多卖出相同面积的苗木.下表为2001年、2002年、2003年三年种植苗木与卖出成苗木的面积统计数据.
假设所有苗木的成活率都是100%,问到哪一年年底,这个镇的苗木面积达到5万亩?
查看习题详情和答案>>
在计算1+4+7+10+13+16+19+22+25+28时,我们发现,从第一个数开始,以后的每个数与它的前一个数的差都是一个相同的定值,具有这种规律的一列数,求和时,除了直接相加外,我们还可以用公式S=na+
| n(n-1) |
| 2 |
| 10(10-1) |
| 2 |
用上面的知识解决下列问题:
我市某乡镇具有“中国北方乔木之乡”的美称,到2000年底这个镇已有苗木2万亩,为增加农民收入,这个镇实施“苗木兴镇”战略,逐年有计划地扩种苗木.从2001年起,以后每年又比上一年多种植相同面积的苗木;从2001年起每年卖出成苗木,以后每年又比上一年多卖出相同面积的苗木.下表为2001年、2002年、2003年三年种植苗木与卖出成苗木的面积统计数据.
| 年份 | 2001年 | 2002年 | 2003年 |
| 每年种植苗木的面积(亩) | 4000 | 5000 | 6000 |
| 每年卖出成苗木的面积(亩) | 2000 | 2500 | 3000 |
将 绕点
绕点 按逆时针方向旋转,旋转角为
按逆时针方向旋转,旋转角为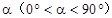 ,旋转后使各边长变为原来的
,旋转后使各边长变为原来的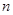 倍,得到
倍,得到 ,我们将这种变换记为[
,我们将这种变换记为[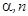 ].
].
(1)如图①,对 作变换[
作变换[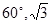 ]得
]得 ,则
,则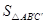 :
: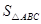 = ___;直线
= ___;直线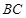 与直线
与直线 所夹的锐角为 __ °;
所夹的锐角为 __ °;

图①
(2)如图②, 中,
中,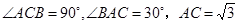 ,对
,对 作变换[
作变换[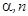 ]得
]得 ,使得四边形
,使得四边形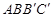 为梯形,其中
为梯形,其中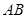 ∥
∥ ,且梯形
,且梯形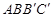 的面积为
的面积为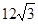 ,求
,求 和
和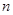 的值.
的值.

图②
查看习题详情和答案>>
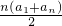 (其中n表示数的个数,a1表示第一个数,an表示最后一个数),所以1+4+7+10+13+16+19+22+25+28=
(其中n表示数的个数,a1表示第一个数,an表示最后一个数),所以1+4+7+10+13+16+19+22+25+28=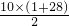 =145.
=145.