摘要： 如图.在矩形ABCD中.AD=8,点E是AB边上的一点.AE=,过D,E两点作直线PQ.与BC边所在的直线MN相交于点F.(1)求tan∠ADE的值,(2)点G是线段AD上的一个动点.GH⊥DE垂足为H.设DG为x.四边形AEHG的面积为y.请求出y与x之间的函数关系式,
网址：http://m.1010jiajiao.com/timu_id_659169[举报]
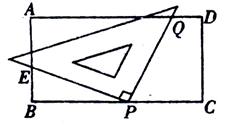
如图，在矩形ABCD中，AD=12cm,AB=
，三角形的直角形顶点P在线段BC上，一直角边与线段AD的交点为Q，另一直角边与线段AB的交点为E，点P从C开始向B以2cm/s的速度运动，点Q从D开始以1cm/s的速度向点A运动，假设P、Q两点开始运动，运动时间为ts.
(1)当t=1，
时，PQ的长是多少？
（2）当
时，点Q运动多长时间点E与A重合？
（3）当
时，①设BE的长为y cm，试求
之间的函数关系式.②是否存在某个时刻，使点E与点A重合？若存在，求出点P、点Q的运动时间；若不存在，请求出AE的最小值.
如图，在矩形ABCD中，AD=8，点E是AB边上的一点，AE=2
，过D、E两点作直线PQ，与BC边所在的直线MN相交点F．
（1）求tan∠ADE的值；
（2）点G是线段AD上的一个动点（不运动至点A、D），GH⊥DE垂足为H，设DG为x，四边形AEHG的面积为y；请求出y与x之间的函数关系式；
（3）如果AE=2EB，点O是直线MN上的一个动点，以O为圆心作圆，使⊙O与直线PQ相切，同时又与矩形ABCD的某一边相切，问满足条件的⊙O有几个？并请求出其中一个圆的半径．
，过D、E两点作直线PQ，与BC边所在的直线MN相交点F． （1）求tan∠ADE的值；
（2）点G是线段AD上的一个动点（不运动至点A、D），GH⊥DE垂足为H，设DG为x，四边形AEHG的面积为y；请求出y与x之间的函数关系式；
（3）如果AE=2EB，点O是直线MN上的一个动点，以O为圆心作圆，使⊙O与直线PQ相切，同时又与矩形ABCD的某一边相切，问满足条件的⊙O有几个？并请求出其中一个圆的半径．
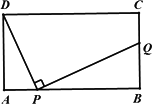
如图，在矩形ABCD中，AD＝4，AB＝m(m＞4)，点P是AB边上的任意一点(不与A、B重合)，连结PD，过点P作PQ⊥PD，交直线BC于点Q．
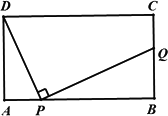
(1)当m＝10时，是否存在点P使得点Q与点C重合？若存在，求出此时AP的长；若不存在，说明理由；
(2)连结AC，若PQ∥AC，求线段BQ的长(用含m的代数式表示)
(3)若△PQD为等腰三角形，求以P、Q、C、D为顶点的四边形的面积S与m之间的函数关系式，并写出m的取值范围．
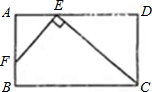20、如图，在矩形ABCD中，E是AD边上点，∠CEF=90°，EF交AB边与F，