某校500名学生参加一次测试，测试分数均大于或等于60且小于100，分数段的频率分布情况如表所示（其中每个分数段可包括最小值，不包括最大值），测试分数在70～80分数段的学生有    名．

某校组织初三学生电脑技能竞赛，每班参加比赛的学生人数相同，竞赛成绩分为A、B、C、D四个等级，其中相应等级的得分依次记为100分，90分，80分，70分．将初三(1)班和(2)班的成绩整理并绘制成统计图如下．

（1）此次竞赛中（2）班成绩在C级以上（包括C级）的人数为        ；

（2）请你将表格补充完整：

（3）试运用所学的统计知识，从二个不同角度评价初三（1）班和初三（2）班的成绩．

请尝试解决以下问题：

（1）如图1，在正方形ABCD中，点E，F分别为DC，BC边上的点，且满足∠EAF=45°，连接EF，求证DE+BF=EF．

感悟解题方法，并完成下列填空：

将△ADE绕点A顺时针旋转90°得到△ABG，此时AB与AD重合，

由旋转可得：AB=AD,BG=DE, ∠1=∠2，∠ABG=∠D=90°,

∴∠ABG+∠ABF=90°+90°=180°，

因此，点G，B，F在同一条直线上．

∵∠EAF=45°  ∴∠2+∠3=∠BAD-∠EAF=90°-45°=45°．

∵∠1=∠2，   ∴∠1+∠3=45°．

即∠GAF=∠_________．

又AG=AE，AF=AF

∴△GAF≌_______．

∴_________=EF，故DE+BF=EF．

（2）运用（1）解答中所积累的经验和知识，完成下题：

如图2，在直角梯形ABCD中，AD∥BC（AD＞BC），∠D＝90°，AD＝CD＝10，E是CD上一点，且∠BAE＝45°，DE＝4，求BE的长．

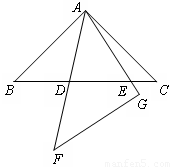
（2）类比（1）证明思想完成下列问题：在同一平面内，将两个全等的等腰直角三角形ABC和AFG摆放在一起，A为公共顶点，∠BAC=∠AGF=90°，若∆ABC固定不动，∆AFG绕点A旋转，AF、AG与边BC的交点分别为D、E(点D不与点B重合，点E不与点C重合)，在旋转过程中，等式BD+CE=DE始终成立，请说明理由．

某中学七年级学生共450人，其中男生250人，女生200人。该校对七年级所有学生进行了一次体育测试，并随即抽取了50名男生和40名女生的测试成绩作为样本进行分析，绘制成如下的统计表：

（1）请解释“随即抽取了50名男生和40名女生”的合理性；

（2）从上表的“频数”、“百分比”两列数据中选择一列，用适当的统计图表示；

（3）估计该校七年级学生体育测试成绩不合格的人数。

为了了解全区近6000名初三学生数学学习状况，随机抽取600名学生的测试成绩作为样本，将他们的成绩整理后分组情况如下：（每组数据含最低值，不含最高值）

根据上表信息，由此样本请你估计全区此次测试成绩在70～80分的人数大约是           ．