摘要:(1)求菱形的面积,
网址:http://m.1010jiajiao.com/timu_id_654153[举报]
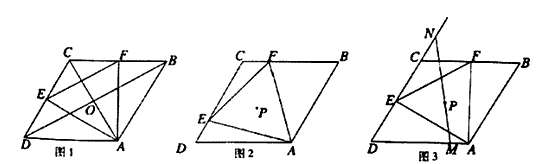
已知菱形ABCD的边长为1.∠ADC=60°,等边△AEF两边分别交边DC、CB于点E、F.
(1)特殊发现:如图1,若点E、F分别是边DC、CB的中点.求证:菱形ABCD对角线AC、BD交点O即为等边△AEF的外心;
(2)若点E、F始终分别在边DC、CB上移动.记等边△AEF的外心为点P.
①猜想验证:如图2.猜想△AEF的外心P落在哪一直线上,并加以证明;
②拓展运用:如图3,当△AEF面积最小时,过点P任作一直线分别交边DA于点M,交边DC的延长线于点N,试判断
+
是否为定值?若是,请求出该定值;若不是,请说明理由.
 查看习题详情和答案>>
查看习题详情和答案>>
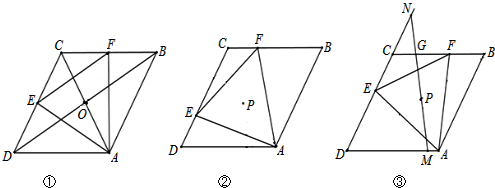
(1)特殊发现:如图1,若点E、F分别是边DC、CB的中点.求证:菱形ABCD对角线AC、BD交点O即为等边△AEF的外心;
(2)若点E、F始终分别在边DC、CB上移动.记等边△AEF的外心为点P.
①猜想验证:如图2.猜想△AEF的外心P落在哪一直线上,并加以证明;
②拓展运用:如图3,当△AEF面积最小时,过点P任作一直线分别交边DA于点M,交边DC的延长线于点N,试判断
| 1 |
| DM |
| 1 |
| DN |
 查看习题详情和答案>>
查看习题详情和答案>>
已知菱形ABCD的边长为1.∠EAF=∠ADC=60°,∠EAF的两边分别交边DC、CB于点E、F.当∠EAF绕点A旋转时,点E、F始终分别在边DC、CB上移动.
(1)特殊发现:如图1,若点E、F分别是边DC、CB的中点.求证:菱形ABCD对角线AC、BD交点O即为△AEF的外心;
(2)记△AEF的外心为点P.
①如图2.求证:△AEF为等边三角形;
②猜想验证:如图2.猜想△AEF的外心P落在哪一直线上,并加以证明;
(3)拓展运用:如图3,当△AEF面积最小时,过点P任作一直线分别交边DA于点M,交边DC的延长线于点N,当MN⊥AD于M时,
+
的值为

查看习题详情和答案>>
(1)特殊发现:如图1,若点E、F分别是边DC、CB的中点.求证:菱形ABCD对角线AC、BD交点O即为△AEF的外心;
(2)记△AEF的外心为点P.
①如图2.求证:△AEF为等边三角形;
②猜想验证:如图2.猜想△AEF的外心P落在哪一直线上,并加以证明;
(3)拓展运用:如图3,当△AEF面积最小时,过点P任作一直线分别交边DA于点M,交边DC的延长线于点N,当MN⊥AD于M时,
| 1 |
| DM |
| 1 |
| DN |
2
2
.
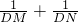 是否为定值?若是,请求出该定值;若不是,请说明理由.
是否为定值?若是,请求出该定值;若不是,请说明理由.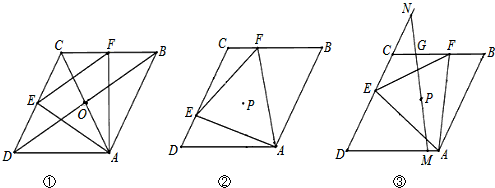
 是否为定值,若是,请求出该定值;若不是,请说明理由。
是否为定值,若是,请求出该定值;若不是,请说明理由。