摘要：(2)若销售利润为.请写出与之间的函数关系式.并求出销售价为每吨2万元时的销售利润.29?.为了解决农民工子女入学难的问题.我市建立了一套进城农民工子女就学的保障机制.其中一项就是免交“借读费 .据统计.2004年秋季有5000名农民工子女进入主城区中小学学习.预测2005年秋季进入主城区中小学学习的农民工子女将比2004年有所增加.其中小学增加20%.中学增加30%.这样.2005年秋季将新增1160名农民工子女在主城区中小学学习. (1)如果按小学每生每年收“借读费 500元.中学每生每年收“借读费 1000元计算.求2005年新增的1160名中小学生共免收多少“借读费 ? (2)如果小学每40名学生配备2名教师.中学每40名学生配备3名教师.若按2005年秋季入学后.农民工子女在主城区中小学就读的学生人数计算.一共需要配备多少名中小学教师?30?.如图.AB是△ABC的外接圆⊙O的直径.D是⊙O上的一点.DE⊥AB于点E.且DE的延长线分别交AC.⊙O.BC的延长线于F.M.G. (1)求证:AE?BE＝EF?EG, (2)连结BD.若BD⊥BC.且EF＝MF＝2.求AE和MG的长.
网址：http://m.1010jiajiao.com/timu_id_653510[举报]
新年伊始，武汉市商品房销售量降至冰点．某楼盘2月份的成交均价为6000元/㎡，销售量仅为20套．为了增加销售量，该楼盘采用了降价的促销方式（但降幅不得超过20%）．据目前的市场规律，若此楼盘每平方米降价50元，则每月可多卖出一套．假设每套面积均为100㎡，每平方米的成本为2000元．
（1）设每平方米降价x元（x为50的整数倍），每月利润为y元，请求出y与x之间的函数关系式，并写出自变量的取值范围；
（2）月利润能否达到1250万元？若能，售价是多少；若不能，请说明理由；
（3）若月利润不低于1050万元，请直接写出每平方米售价a的取值范围． 查看习题详情和答案>>
（1）设每平方米降价x元（x为50的整数倍），每月利润为y元，请求出y与x之间的函数关系式，并写出自变量的取值范围；
（2）月利润能否达到1250万元？若能，售价是多少；若不能，请说明理由；
（3）若月利润不低于1050万元，请直接写出每平方米售价a的取值范围． 查看习题详情和答案>>
新年伊始，武汉市商品房销售量降至冰点．某楼盘2月份的成交均价为6000元/㎡，销售量仅为20套．为了增加销售量，该楼盘采用了降价的促销方式（但降幅不得超过20%）．据目前的市场规律，若此楼盘每平方米降价50元，则每月可多卖出一套．假设每套面积均为100㎡，每平方米的成本为2000元．
（1）设每平方米降价x元（x为50的整数倍），每月利润为y元，请求出y与x之间的函数关系式，并写出自变量的取值范围；
（2）月利润能否达到1250万元？若能，售价是多少；若不能，请说明理由；
（3）若月利润不低于1050万元，请直接写出每平方米售价a的取值范围．
查看习题详情和答案>>
淮安华宇公司获得授权生产某种奥运纪念品，经市场调查分析，该纪念品的销售量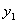
（万件）与纪念品的价格
（元／件）之间的函数图象如图所示，该公司纪念品的生产数量
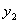（万件）与纪念品的价格
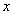（元／件）近似满足函数关系式
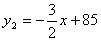，若每件纪念品的价格不小于20元，且不大于40元。请解答下列问题：
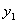（万件）与纪念品的价格（元／件）之间的函数图象如图所示，该公司纪念品的生产数量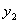（万件）与纪念品的价格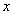（元／件）近似满足函数关系式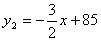，若每件纪念品的价格不小于20元，且不大于40元。请解答下列问题：
（1）求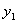
与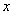
的函数关系式，并写出
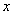的取值范围；
（2）若每件纪念品的成本为15元，则价格应定为多少元时，能获得最大利润？并求出此时的最大利润。
查看习题详情和答案>>
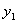与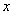的函数关系式，并写出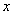的取值范围；（2）若每件纪念品的成本为15元，则价格应定为多少元时，能获得最大利润？并求出此时的最大利润。
新年伊始，武汉市商品房销售量降至冰点．某楼盘2月份的成交均价为6000元/㎡，销售量仅为20套．为了增加销售量，该楼盘采用了降价的促销方式（但降幅不得超过20%）．据目前的市场规律，若此楼盘每平方米降价50元，则每月可多卖出一套．假设每套面积均为100㎡，每平方米的成本为2000元．
（1）设每平方米降价x元（x为50的整数倍），每月利润为y元，请求出y与x之间的函数关系式，并写出自变量的取值范围；
（2）月利润能否达到1250万元？若能，售价是多少；若不能，请说明理由；
（3）若月利润不低于1050万元，请直接写出每平方米售价a的取值范围．
查看习题详情和答案>>
（1）设每平方米降价x元（x为50的整数倍），每月利润为y元，请求出y与x之间的函数关系式，并写出自变量的取值范围；
（2）月利润能否达到1250万元？若能，售价是多少；若不能，请说明理由；
（3）若月利润不低于1050万元，请直接写出每平方米售价a的取值范围．
查看习题详情和答案>>
银川市某企业为某计算机产业基地提供电脑配件．受美元走低的影响，从去年1至9月（前年12月份原材料价格540元/件），该配件的原材料价格一路攀升，每件配件的原材料价格y1(元)与月份x(1≤x≤9，且x取整数)之间的函数关系如下表：
| 月份x | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
| 价格y1(元/件) | 560 | 580 | 600 | 620 | 640 | 660 | 680 | 700 | 720 |
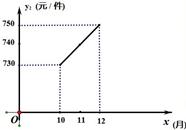
(1)请观察题中的表格，用所学过的一次函数、反比例函数或二次函数的有关知识，直接写出y1与x之间的函数关系式，根据如图所示的变化趋势，直接写出y2与x之间满足的一次函数关系式；
(2)若去年该配件每件的售价为1000元，生产每件配件的人力成本为50元，其它成本30元，该配件在1至9月的销售量p1(万件)与月份x满足关系式p1＝0.1x＋1.1(1≤x≤9，且x取整数)，10至12月的销售量p2(万件)p2＝－0.1x＋2.9(10≤x≤12，且x取整数)．分别求出去年4月份和10月份每个月销售该配件的利润，并比较那个月的利润大；
(3)今年1至5月，每件配件的原材料价格均比去年12月上涨60元，人力成本比去年增加20%，其它成本没有变化，该企业将每件配件的售价在去年的基础上提高a%，与此同时每月销售量均在去年12月的基础上减少0.1 a%.这样，在保证每月上万件配件销量的前提下，完成1至5月的总利润1700万元的任务，请你参考以下数据，估算出a的整数值．(参考数据：992＝9801，982＝9604，972＝9409，962＝9216，952＝9025) 查看习题详情和答案>>