摘要：(1)请在横线上直接写出抛物线的解析式: ,
网址：http://m.1010jiajiao.com/timu_id_650312[举报]
已知抛物线C1：y=-x2+2mx+n（m，n为常数，且m≠0，n＞0）的顶点为A，与y轴交于点C；抛物线C2与抛物线C1关于y轴对称，其顶点为B，连接AC，BC，AB．
注：抛物线y=ax2+bx+c（a≠0）的顶点坐标为(-
，
)．
（1）请在横线上直接写出抛物线C2的解析式： ；
（2）当m=1时，判定△ABC的形状，并说明理由；
（3）抛物线C1上是否存在点P，使得四边形ABCP为菱形？如果存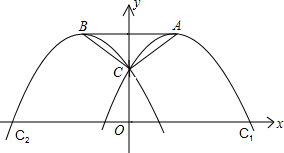
在，请求出m的值；如果不存在，请说明理由．
查看习题详情和答案>>
注：抛物线y=ax2+bx+c（a≠0）的顶点坐标为(-
| b |
| 2a |
| 4ac-b2 |
| 4a |
（1）请在横线上直接写出抛物线C2的解析式：
（2）当m=1时，判定△ABC的形状，并说明理由；
（3）抛物线C1上是否存在点P，使得四边形ABCP为菱形？如果存
在，请求出m的值；如果不存在，请说明理由．
查看习题详情和答案>>
已知抛物线C1：y=-x2+2mx+n（m，n为常数，且m≠0，n＞0）的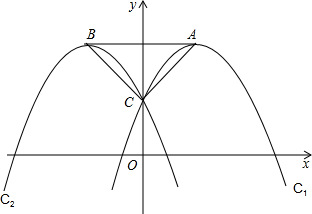
顶点为A，与y轴交于点C；抛物线C2与抛物线C1关于y轴对称，其顶点为B，连接AC，BC，AB．
（1）请在横线上直接写出抛物线C2的解析式： ；
（2）当m=1时，判定△ABC的形状，并说明理由；
（3）抛物线C1上是否存在点P，使得四边形ABCP为菱形？如果存在，请求出m的值；如果不存在，请说明理由． 查看习题详情和答案>>
顶点为A，与y轴交于点C；抛物线C2与抛物线C1关于y轴对称，其顶点为B，连接AC，BC，AB．（1）请在横线上直接写出抛物线C2的解析式：
（2）当m=1时，判定△ABC的形状，并说明理由；
（3）抛物线C1上是否存在点P，使得四边形ABCP为菱形？如果存在，请求出m的值；如果不存在，请说明理由． 查看习题详情和答案>>
24、已知抛物线m：y=ax2+bx+c （a≠0） 与x轴交于A、B两点（点A在左），与y轴交于点C，顶点为M，抛物线上部分点的横坐标与对应的纵坐标如下表：| x | … | -2 | 0 | 2 | 3 | … |
| y | … | 5 | -3 | -3 | 0 | … |
（2）若将抛物线m，绕原点O顺时针旋转180°，试写出旋转后抛物线n的解析式，并在坐标系中画出抛物线m、n的草图；
（3）若抛物线n的顶点为N，与x轴的交点为E、F（点E、F分别与点A、B对应），试问四边形NFMB是何种特殊四边形？并说明其理由．
已知抛物线y=ax2+bx+c（a≠0）与x轴交点的横坐标分别为-1，3，与y轴交点的纵坐标为