网址:http://m.1010jiajiao.com/timu_id_64904[举报]
、已知集合A={12, 14, 16, 18, 20},B={11, 13, 15, 17, 19},在A中任取一个元素ai(i=1, 2, 3, 4, 5),在B中任取一个元素bj ( j =1, 2, 3, 4, 5),则所取两数ai、bj满足ai>bj的概率为 .
查看习题详情和答案>>
、已知集合A={12, 14, 16, 18, 20},B={11, 13, 15, 17, 19},在A中任取一个元素ai(i=1, 2, 3, 4, 5),在B中任取一个元素bj ( j =1, 2, 3, 4, 5),则所取两数ai、bj满足ai>bj的概率为 .
查看习题详情和答案>>
对甲、乙两种商品的重量的误差进行抽查,测得数据如下(单位:mg):
甲:13 15 1 4 14 9 14 21 9 10 11
乙:10 14 9 12 15 14 11 19 22 16
(Ⅰ)画出样本数据的茎叶图,并指出甲,乙两种商品重量误差的中位数;
(Ⅱ)计算甲种商品重量误差的样本方差;
(Ⅲ)现从重量误差不低于15的乙种商品中随机抽取两件,求重量误差为19的商品被抽中的概率.
查看习题详情和答案>>
(本题满分15分)杨辉是中国南宋末年的一位杰出的数学家、数学教育家,杨辉三角是杨辉的一大重要研究成果,它的许多性质与组合数的性质有关,杨辉三角中蕴藏了许多优美的规律.下图是一个11阶杨辉三角: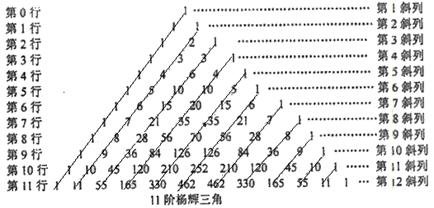
(1)求第20行中从左到右的第3个数;
(2)若第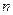 行中从左到右第13与第14个数的比为
行中从左到右第13与第14个数的比为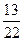 ,求
,求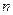 的值;
的值;
(3)写出第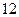 行所有数的和,写出
行所有数的和,写出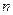 阶(包括
阶(包括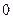 阶)杨辉三角中的所有数的和;
阶)杨辉三角中的所有数的和;
(4)在第3斜列中,前5个数依次为1,3,6,10,15;第4斜列中,第5个数为35,我们发现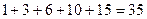 ,事实上,一般地有这样的结论:第
,事实上,一般地有这样的结论:第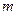 斜列中(从右上到左下)前
斜列中(从右上到左下)前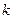 个数之和,一定等于第
个数之和,一定等于第 斜列中第
斜列中第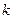 个数.
个数.
试用含有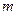 ,
,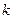
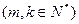 的数学式子表示上述结论,并证明.
的数学式子表示上述结论,并证明.
(本题满分15分)杨辉是中国南宋末年的一位杰出的数学家、数学教育家,杨辉三角是杨辉的一大重要研究成果,它的许多性质与组合数的性质有关,杨辉三角中蕴藏了许多优美的规律.下图是一个11阶杨辉三角:
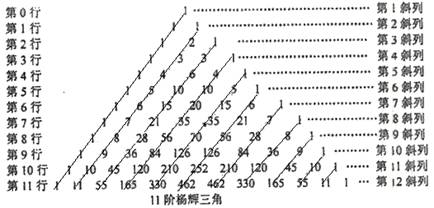
(1)求第20行中从左到右的第3个数;
(2)若第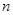 行中从左到右第13与第14个数的比为
行中从左到右第13与第14个数的比为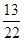 ,求
,求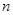 的值;
的值;
(3)写出第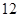 行所有数的和,写出
行所有数的和,写出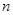 阶(包括
阶(包括 阶)杨辉三角中的所有数的和;
阶)杨辉三角中的所有数的和;
(4)在第3斜列中,前5个数依次为1,3,6,10,15;第4斜列中,第5个数为35,我们发现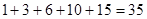 ,事实上,一般地有这样的结论:第
,事实上,一般地有这样的结论:第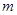 斜列中(从右上到左下)前
斜列中(从右上到左下)前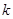 个数之和,一定等于第
个数之和,一定等于第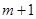 斜列中第
斜列中第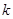 个数.
个数.
试用含有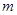 ,
,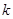
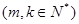 的数学式子表示上述结论,并证明.
的数学式子表示上述结论,并证明.
查看习题详情和答案>>