摘要:解析:由切割线定理得:. . ..
网址:http://m.1010jiajiao.com/timu_id_64753[举报]
已知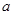 ,
,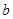 ,
,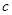 分别为
分别为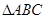 三个内角
三个内角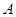 ,
,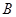 ,
,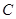 的对边,
的对边, .
.
(Ⅰ)求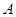 ;
;
(Ⅱ)若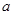 =2,
=2,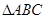 的面积为
的面积为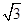 ,求
,求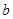 ,
,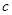 .
.
【命题意图】本题主要考查正余弦定理应用,是简单题.
【解析】(Ⅰ)由 及正弦定理得
及正弦定理得
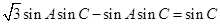
由于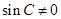 ,所以
,所以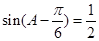 ,
,
又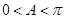 ,故
,故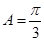 .
.
(Ⅱ) 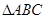 的面积
的面积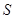 =
=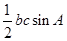 =
=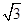 ,故
,故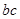 =4,
=4,
而 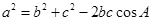 故
故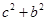 =8,解得
=8,解得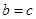 =2
=2
查看习题详情和答案>>
过抛物线

 的对称轴上的定点
的对称轴上的定点 ,作直线
,作直线 与抛物线相交于
与抛物线相交于 两点.
两点.
(I)试证明 两点的纵坐标之积为定值;
两点的纵坐标之积为定值;
(II)若点 是定直线
是定直线 上的任一点,试探索三条直线
上的任一点,试探索三条直线 的斜率之间的关系,并给出证明.
的斜率之间的关系,并给出证明.
【解析】本题主要考查抛物线与直线的位置关系以及发现问题和解决问题的能力.
(1)中证明:设 下证之:设直线AB的方程为: x=ty+m与y2=2px联立得消去x得y2=2pty-2pm=0,由韦达定理得
下证之:设直线AB的方程为: x=ty+m与y2=2px联立得消去x得y2=2pty-2pm=0,由韦达定理得

(2)中:因为三条直线AN,MN,BN的斜率成等差数列,下证之
设点N(-m,n),则直线AN的斜率KAN= ,直线BN的斜率KBN=
,直线BN的斜率KBN=

KAN+KBN= +
+
本题主要考查抛物线与直线的位置关系以及发现问题和解决问题的能力.
查看习题详情和答案>>