网址:http://m.1010jiajiao.com/timu_id_64168[举报]
一、选择题(每小题5分,共60分)
BDACC ACDDB AA
二、填空题(每小题4分,共16分)
13. 14.
14. 15.
15. 16.②③
16.②③
三、解答题(共74分)
17.解:(I)由正弦定理 ,有
,有

代入 得
得
即



(Ⅱ)
由 得
得
所以,当 时,
时, 取得最小值为0
取得最小值为0
18.解:(I)由已知得
故
即
故数列 为等比数列,且
为等比数列,且
又当 时,
时,


而 亦适合上式
亦适合上式


(Ⅱ)
所以


19.解:(I)由该四棱锥的三视图可知,该四棱锥 的底面的边长为1的正方
的底面的边长为1的正方
侧棱 底面
底面 ,且
,且 ,
,
(Ⅱ)连结 交
交 于
于 ,则
,则 为
为 的中点,
的中点,
 为
为 的中点,
的中点,
 ,
,
又 平面
平面 内,
内,
 平面
平面
 (Ⅲ)不论点E在何位置,都有
(Ⅲ)不论点E在何位置,都有
证明:连结 是正方形,
是正方形,
 底面
底面 ,且
,且 平面
平面 ,
,

又 平面
平面
 不论点
不论点 在何位置,都有
在何位置,都有 平面
平面
 不论点E在何位置,都有
不论点E在何位置,都有 。
。
20.解:
(I)利用树形图我们可以列出连续抽取2张卡片的所有可能结果(如下图所示)。

由上图可以看出,实验的所有可能结果数为20,因为每次都随机抽取,因此这20种结果出现的可能性是相同的,实验属于古典概型。 用 表示事“连续抽取2人都是女生”。则
表示事“连续抽取2人都是女生”。则 与
与 互斥,并且
互斥,并且 表示事件“连续抽取2张卡片,取出的2人不全是男生”,由列出的所有可能结果可以看出,
表示事件“连续抽取2张卡片,取出的2人不全是男生”,由列出的所有可能结果可以看出, 的结果有12种,
的结果有12种, 的结果有2种,由互斥事件的概率加法公式,可得
的结果有2种,由互斥事件的概率加法公式,可得

即连续抽取2张卡片,取出的2人不全是男生的概率为0.7
(Ⅱ)有放回地连续抽取2张卡片,需注意同一张卡片可再次被取出,并且它被取出的可能性和其他卡片相等,我们用一个有序实数对表示抽取的结果,例如“第一次取出2号,第二次取出4号”就用(2,4)来表示,所有的可能结果可以用下表列出。
 第二次抽取
第二次抽取
第一次抽取
1
2
3
4
5
1
(1,1)
(1,2)
(1,3)
(1,4)
(1,5)
2
(2,1)
(2,2)
(2,3)
(2,4)
(2,5)
3
(3,1)
(3,2)
(3,3)
(3,4)
(3,5)
4
(4,1)
(4,2)
(4,3)
(4,4)
(4,5)
5
(5,1)
(5,2)
(5,3)
(5,4)
(5,5)
实验的所有可能结果数为25,并且这25种结果出现的可能性是相同的,实验属于古典型。
用 表示事件“独唱和朗诵由同一个人表演”,由上表可以看出,
表示事件“独唱和朗诵由同一个人表演”,由上表可以看出, 的结果共
的结果共
有5种,因次独唱和朗诵由同一个人表演的概率

21.解:
(I)
依题意由
即 解得
解得

 ,得
,得
 的单调递减区间是
的单调递减区间是
(Ⅱ)由 得
得
 不等式组确定的平面区域如图阴影部分所示;
不等式组确定的平面区域如图阴影部分所示;
由 得
得
 不等式组确定的平面区域如图阴影部分所示;
不等式组确定的平面区域如图阴影部分所示;
由 得
得
 点的坐标为(0,-1)
点的坐标为(0,-1)
设 ,则
,则 表示平面区域内的点
表示平面区域内的点 与点
与点
 连线斜率。
连线斜率。
 ,由图可知
,由图可知 或
或
即
22.解:(I)设椭圆方程为
则根据题意,双曲线的方程为
 且满足
且满足
 解方程组得
解方程组得
 椭圆的方程为
椭圆的方程为 ,双曲线的方程
,双曲线的方程
(Ⅱ)由(I)得
设 ,则由
,则由 得
得 为
为 的中点,所以
的中点,所以 点坐标为
点坐标为
 ,
,
将 、
、 坐标代入椭圆和双曲线方程,得
坐标代入椭圆和双曲线方程,得

消去 ,得
,得
解之得 或
或 (舍)
(舍)
所以 ,由此可得
,由此可得 ,
,
所以
当 为
为 时,直线
时,直线 的方程是
的方程是
即:
代入 ,得
,得
所以 或-5(舍)
或-5(舍)
所以 ,
,
 轴。
轴。
所以
已知定义在R上的单调函数![]() ,存在实数
,存在实数![]() ,使得对于任意实数
,使得对于任意实数![]() ,总有
,总有![]() 恒成立。
恒成立。
(Ⅰ)求![]() 的值;
的值;
(Ⅱ)若![]() ,且对任意正整数
,且对任意正整数![]() ,有
,有![]() , ,求数列{an}的通项公式;
, ,求数列{an}的通项公式;
(Ⅲ)若数列{bn}满足![]() ,将数列{bn}的项重新组合成新数列
,将数列{bn}的项重新组合成新数列![]() ,具体法则如下:
,具体法则如下:![]()
![]() ……,求证:
……,求证:![]() 。
。
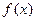 ,存在实数
,存在实数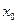 ,使得对于任意实数
,使得对于任意实数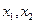 ,总有
,总有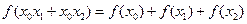 恒成立。
恒成立。(Ⅰ)求
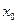 的值;
的值;(Ⅱ)若
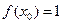 ,且对任意正整数
,且对任意正整数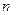 ,有
,有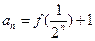 , ,求数列{an}的通项公式;
, ,求数列{an}的通项公式;(Ⅲ)若数列{bn}满足
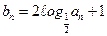 ,将数列{bn}的项重新组合成新数列
,将数列{bn}的项重新组合成新数列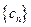 ,具体法则如下:
,具体法则如下: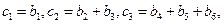
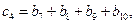 ……,求证:
……,求证: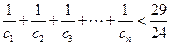 。
。已知数列![]() 的各项均为正数,
的各项均为正数,![]() 为其前n项和,对于任意
为其前n项和,对于任意![]() ,满足关系
,满足关系![]() 。
。
(Ⅰ)求数列![]() 的通项公式;
的通项公式;
(Ⅱ)设数列![]() 的前n项和为
的前n项和为![]() ,且
,且![]() ,求证:对任意正整数n,总有
,求证:对任意正整数n,总有![]() 。
。
(Ⅲ)在正数数列![]() 中,设
中,设![]() ,求数列
,求数列![]() 中的最大项。
中的最大项。
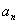 }的各项均为正数,
}的各项均为正数,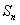 为其前n项和,对于任意的n∈N*,满足关系式2
为其前n项和,对于任意的n∈N*,满足关系式2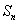 =3
=3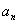 -3。
-3。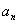 }的通项公式;
}的通项公式; }的通项公式是
}的通项公式是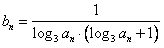 ,前n项和为Tn,求证:对于任意的正整数n,总有Tn<1。
,前n项和为Tn,求证:对于任意的正整数n,总有Tn<1。 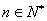 ,满足关系式2Sn=3an-3。
,满足关系式2Sn=3an-3。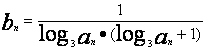 ,前n项和为Tn,求证:对于任意的正整数n,总有Tn<1
,前n项和为Tn,求证:对于任意的正整数n,总有Tn<1