网址:http://m.1010jiajiao.com/timu_id_63762[举报]
一、选择题(5分×12=60分)
B B D D C B B D D C A A
二、填空题(4分x 4=16分)
13.80 14.32 15. 16.①③
16.①③
三、解答题(12分×5+14分=74分)
17.解:(1) 2分
2分
 ……………………4分
……………………4分
 ∴
∴ 的最小正周期为
的最小正周期为 …………………6分
…………………6分
(2)∵ 成等比数列 ∴
成等比数列 ∴ 又
又
∴ ……………………………………4分
……………………………………4分
又∵ ∴
∴ ……………………………………………………10分
……………………………………………………10分
 ……………………………………12分
……………………………………12分
18.解:(1)设 公差
公差 由
由 成等比数列得
成等比数列得 …………………1分
…………………1分
∴即 ∴
∴ 舍去或
舍去或 …………………………3分
…………………………3分
∴ ………………………………………………4分
………………………………………………4分
∴ ………………………………………………6分
………………………………………………6分
(2) ∵ ………………………………………………7分
………………………………………………7分
∴ …①
…………8分
…①
…………8分
 …………②
…………9分
…………②
…………9分
①-②得:

∴ ………………………………………………12分
………………………………………………12分
19.解:(1)记“任取2张卡片,将卡片上的函数相加得到偶函数”为事件A,
 ……………………………………………………4分
……………………………………………………4分
(2)设符合题设条件,抽取次数恰为3的事件记为B,则
 ………………………………………………12分
………………………………………………12分
20.解:(1)连结

 为正△
…1分
为正△
…1分






 面
面
 3分
3分
面 面
面



即点 的位置在线段
的位置在线段 的四等分点且靠近
的四等分点且靠近 处 ………………………………………6分
处 ………………………………………6分
(2)过 作
作 于
于 ,连
,连
 由(1)知
由(1)知 面
面 (三垂线定理)
(三垂线定理)
∴ 为二面角
为二面角 的平面角……9分
的平面角……9分




在 中,
中,
在 中,
中,
∴二面角 的大小为
的大小为 ………………………………………12分
………………………………………12分
(说明:若用空间向量解,请参照给分)
21.解:(1) 由
由 得
得 ……2分
……2分
①当 时,
时, 在
在 内是增函数,故无最小值………………………3分
内是增函数,故无最小值………………………3分
 ②当
②当 时,
时,
 在
在 处取得极小值
处取得极小值 ………………………5分
………………………5分


由
解得: ≤
≤ ∴
∴ ≤
≤
 …………6分
…………6分
 ≥
≥
(2)由(1)知 在区间
在区间 上均为增函数
上均为增函数
又 ,故要在
,故要在 内
内 为增函数
为增函数


 ≤
≤
 ≥
≥
必须: 或 ………………………………………10分
 ≤
≤
 ≤
≤
 ∴
∴ ≤
≤ 或
或 ≥
≥ ∴实数
∴实数 的取值范围是:
的取值范围是: …………………12分
…………………12分
22.解:(1)如图,设 为椭圆的下焦点,连结
为椭圆的下焦点,连结
∴ ∵
∵ ∴
∴ …3分
…3分
∵ ∴
∴ ………4分
………4分
∴ 的离心率为
的离心率为
…………………………………………………………6分
(2)∵ ,∴抛物线方程为:
,∴抛物线方程为: 设点
设点 则
则 ∵
∵
∴ 点处抛物线
点处抛物线 的切线斜率
的切线斜率 ……………………………………………………8分
……………………………………………………8分
则切线 方程为:
方程为: ……………………………………………………9分
……………………………………………………9分
又∵过点 ∴
∴ ∴
∴ ∴
∴
代入椭圆 方程得:
方程得: ……………………………………………………11分
……………………………………………………11分
∴ ≥
≥ ………………13分
………………13分




当且仅当 即 上式取等号


∴此时椭圆的方程为: ………………………………………………14分
………………………………………………14分
给出下列命题:
①不存在实数![]() 使
使![]() 的定义域、值域均为一切实数;
的定义域、值域均为一切实数;
②函数![]() 图象与函数
图象与函数![]() 图象关于直线
图象关于直线![]() 对称;
对称;
③方程![]() 有且只有一个实数根;
有且只有一个实数根;
④![]() 是方程
是方程![]() 表示圆的充分不必要条件.
表示圆的充分不必要条件.
其中真命题的序号是 .(写出所有真命题的序号)
查看习题详情和答案>>| f(x1)+f(x2) | 2 |
(1)判断1是否为函数f(x)=2x+1(-1≤x≤1)的“均值”,请说明理由;
(2)若函数f(x)=ax2-2x(1<x<2,a为常数)存在“均值”,求实数a的取值范围;
(3)若函数f(x)是单调函数,且其值域为区间I.试探究函数f(x)的“均值”情况(是否存在、个数、大小等)与区间I之间的关系,写出你的结论(不必证明). 查看习题详情和答案>>
对于定义域为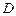 的函数
的函数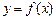 ,若有常数M,使得对任意的
,若有常数M,使得对任意的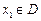 ,存在唯一的
,存在唯一的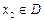 满足等式
满足等式 ,则称M为函数
,则称M为函数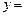 f (x)的“均值”.
f (x)的“均值”.
(1)判断1是否为函数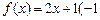 ≤
≤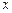 ≤
≤ 的“均值”,请说明理由;
的“均值”,请说明理由;
(2)若函数
 为常数)存在“均值”,求实数a的取值范围;
为常数)存在“均值”,求实数a的取值范围;
(3)若函数 是单调函数,且其值域为区间I.试探究函数
是单调函数,且其值域为区间I.试探究函数 的“均值”情况(是否存在、个数、大小等)与区间I之间的关系,写出你的结论(不必证明).
的“均值”情况(是否存在、个数、大小等)与区间I之间的关系,写出你的结论(不必证明).
说明:对于(3),将根据结论的完整性与一般性程度给予不同的评分
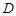 的函数
的函数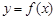 ,若有常数M,使得对任意的
,若有常数M,使得对任意的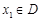 ,存在唯一的
,存在唯一的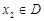 满足等式
满足等式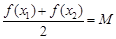 ,则称M为函数
,则称M为函数 f (x)的“均值”.
f (x)的“均值”. ≤
≤ ≤
≤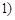 的“均值”,请说明理由;
的“均值”,请说明理由;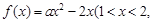
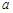 为常数)存在“均值”,求实数a的取值范围;
为常数)存在“均值”,求实数a的取值范围; 是单调函数,且其值域为区间I.试探究函数
是单调函数,且其值域为区间I.试探究函数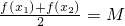 ,则称M为函数y=f (x)的“均值”.
,则称M为函数y=f (x)的“均值”.