网址:http://m.1010jiajiao.com/timu_id_62995[举报]
说明:
一、本解答指出了每题要考查的主要知识和能力,并给出了一种或几种解法供参考,如果考生的解法与本解答不同,可根据试题的主要考查内容比照评分标准制定相应的评分细则.
二、对计算题,当考生的解答在某一步出现错误时,如果后继部分的解答未改变该题的内容和难度,可视影响的程度决定后继部分的给分,但不得超过该部分正确解答应给分数的一半;如果后继部分的解答有较严重的错误,就不再给分.
三、解答右端所注分数,表示考生正确做到这一步应得的累加分数.
四、只给整数分数,选择题和填空题不给中间分.
一、选择题:本题考查基本知识和基本运算,每小题5分,满分50分.
1. A 2. C 3. C 4.C 5.D 6.D 7. B 8. D 9. B 10. C
二、填空题:本题考查基本知识和基本运算,每小题4分,满分20分.
11. 12.38 12. 5 13. 3.files/image278.gif) 14.
14. .files/image280.gif) 15. ②③
15. ②③
三、解答题:本大题共6小题,共80分,解答应写出文字说明,证明过程或演算步骤.
16. 本小题主要考查正弦定理、三角函数的倍角公式、两角和公式等基本知识,考
查学生的运算求解能力. 满分13分.
解:(Ⅰ)由.files/image282.gif) ,知
,知.files/image284.gif) ………………………(2分)
………………………(2分)
又.files/image286.gif) ,得
,得.files/image288.gif) ,
,
.files/image290.gif) ,
,.files/image292.gif) ………………………(5分)
………………………(5分)
故.files/image294.gif) ………………………(6分)
………………………(6分)
(Ⅱ) 由(Ⅰ)知.files/image296.gif) ,
,
.files/image298.gif)
.files/image300.gif)
.files/image302.gif) ………………………………(9分)
………………………………(9分)
.files/image304.gif) ,
,.files/image306.gif)
当.files/image308.gif) ,即
,即.files/image310.gif) 时,
时,.files/image312.gif) 取得最大值为
取得最大值为.files/image314.gif) . ……………(13分)
. ……………(13分)
.files/image316.gif) 17. 本题主要考查线线、线面、面面位置关系,线面角等基本知识,考查空间想像能力,运算求解能力和推理论证能力.
满分13分.
17. 本题主要考查线线、线面、面面位置关系,线面角等基本知识,考查空间想像能力,运算求解能力和推理论证能力.
满分13分.
.files/image317.gif) 解:(Ⅰ)证明:如图,取
解:(Ⅰ)证明:如图,取.files/image319.gif) 中点
中点.files/image321.gif) ,连结
,连结.files/image323.gif) ,
,.files/image325.gif) ;
;
.files/image327.gif)
.files/image323.gif) ∥
∥.files/image330.gif) ,
,.files/image332.gif) ∥
∥.files/image334.gif) ,
,
又.files/image336.gif) ,
,.files/image338.gif) ,
,
.files/image340.gif)
.files/image342.gif) ,…………(3分)
,…………(3分)
四边形.files/image344.gif) 为平行四边形,
为平行四边形,
.files/image346.gif) ∥
∥.files/image325.gif) ,
,
又.files/image349.gif) 平面
平面.files/image179.gif) ,
,.files/image352.gif) 平面
平面.files/image179.gif) ,
,
.files/image346.gif) ∥平面
∥平面.files/image179.gif) .
………………………(6分)
.
………………………(6分)
(Ⅱ)依题意知平面.files/image357.gif) 平面
平面.files/image169.gif) ,
,.files/image360.gif) ,
,
.files/image362.gif) 平面
平面.files/image169.gif) ,得
,得.files/image365.gif)
又.files/image367.gif) ,
,.files/image360.gif) .
.
如图,以.files/image370.gif) 为原点,建立空间直角坐标系
为原点,建立空间直角坐标系.files/image370.gif) -xyz,
-xyz,
.files/image373.gif) ,可得
,可得.files/image375.gif) 、
、.files/image377.gif) 、
、.files/image379.gif) ,
,
.files/image381.gif) .
.
设平面.files/image179.gif) 的一个法向量为
的一个法向量为.files/image384.gif) ,
,
由.files/image386.gif) 得
得.files/image388.gif)
解得.files/image390.gif) ,
,.files/image392.gif) .
………………………(9分)
.
………………………(9分)
设线段.files/image181.gif) 上存在一点
上存在一点.files/image395.gif) ,其中
,其中.files/image397.gif) ,则
,则.files/image399.gif) ,
,
.files/image401.gif) ,
,
依题意:.files/image403.gif) ,即
,即.files/image405.gif) ,
,
可得.files/image407.gif) ,解得
,解得.files/image409.gif) (舍去).
(舍去).
所以.files/image181.gif) 上存在一点
上存在一点.files/image412.gif) . …………(13分)
. …………(13分)
18.本题主要考查函数与导数等基本知识,考查运用数学知识分析问题与解决问题的能力,
考查应用意识. 满分13分.
解:(Ⅰ)依题意,
销售价提高后为6000(1+.files/image048.gif) )元/台,月销售量为
)元/台,月销售量为.files/image415.gif) 台……………(2分)
台……………(2分)
则.files/image417.gif) ……………………(4分)
……………………(4分)
即.files/image419.gif) . ……………………(6分)
. ……………………(6分)
(Ⅱ).files/image421.gif)
令.files/image423.gif) ,得
,得.files/image425.gif) ,
,
解得.files/image427.gif) 舍去).
……………………(9分)
舍去).
……………………(9分)
当.files/image429.gif) 当
当.files/image431.gif)
当.files/image433.gif) 时,
时,.files/image050.gif) 取得最大值.
取得最大值.
此时销售价为.files/image436.gif) 元.
元.
答:笔记本电脑的销售价为9000元时,电脑企业的月利润最大.…………………(13分)
.files/image438.gif) 19.本题主要考查直线与椭圆的位置关系、不等式的解法等基本知识,考查运算求解能力和分析问题、解决问题的能力.
满分13分
19.本题主要考查直线与椭圆的位置关系、不等式的解法等基本知识,考查运算求解能力和分析问题、解决问题的能力.
满分13分
解:(Ⅰ)因为椭圆.files/image148.gif) 的一个焦点是(1,0),所以半焦距
的一个焦点是(1,0),所以半焦距.files/image153.gif) =1.
=1.
因为椭圆两个焦点与短轴的一个端点构成等边三角形.
所以.files/image442.gif) ,解得
,解得.files/image444.gif)
所以椭圆的标准方程为.files/image446.gif) . …(4分)
. …(4分)
.files/image448.gif) (Ⅱ)(i)设直线
(Ⅱ)(i)设直线.files/image063.gif) :
:.files/image451.gif) 与
与.files/image446.gif) 联立并消去
联立并消去.files/image048.gif) 得:
得:.files/image455.gif) .
.
记.files/image457.gif) ,
,.files/image459.gif) ,
,
.files/image461.gif) ,
,
.files/image463.gif) . ……………(5分)
. ……………(5分)
由A关于.files/image048.gif) 轴的对称点为
轴的对称点为.files/image466.gif) ,得
,得.files/image468.gif) ,
,
根据题设条件设定点为.files/image470.gif) (
(.files/image472.gif) ,0),
,0),
得.files/image474.gif) ,即
,即.files/image476.gif) .
.
所以.files/image478.gif)
.files/image480.gif)
即定点.files/image470.gif) (1 ,
0).
……………………………………(8分)
(1 ,
0).
……………………………………(8分)
(ii)由(i)中判别式.files/image483.gif) ,解得
,解得.files/image485.gif) .
.
可知直线.files/image487.gif) 过定点
过定点.files/image470.gif) (1,0).
(1,0).
所以.files/image490.gif) ……………(10分)
……………(10分)
得.files/image492.gif) , 令
, 令.files/image494.gif)
记.files/image496.gif) ,得
,得.files/image498.gif) ,当
,当.files/image500.gif) 时,
时,.files/image502.gif) .
.
.files/image496.gif) 在
在.files/image505.gif) 上为增函数.
上为增函数.
所以.files/image507.gif)
.files/image509.gif) ,
,
得.files/image511.gif) .
.
故△OA1B的面积取值范围是.files/image513.gif) .
……………(13分)
.
……………(13分)
20. 本题主要考查函数的单调性、等差数列、不等式等基本知识,考查运用合理的推理证明解
决问题的方法,考查分类与整合及化归与转化等数学思想. 满分14分.
解:(Ⅰ)因为.files/image515.gif) ,
,
所以.files/image517.gif) .
………………(1分)
.
………………(1分)
(i)当.files/image519.gif) 时,
时,.files/image521.gif) .
.
(ii)当.files/image523.gif) 时,由
时,由.files/image525.gif) ,得到
,得到.files/image527.gif) ,知在
,知在.files/image529.gif) 上
上.files/image521.gif) .
.
(iii)当.files/image532.gif) 时,由
时,由.files/image525.gif) ,得到
,得到.files/image527.gif) ,知在
,知在.files/image536.gif) 上
上.files/image521.gif) .
.
综上,当.files/image539.gif) 时,
时,.files/image541.gif) 递增区间为
递增区间为.files/image536.gif) ;当
;当.files/image523.gif) 时,
时, .files/image545.gif) 递增区间为
递增区间为.files/image547.gif) .
………………………………………(4分)
.
………………………………………(4分)
(Ⅱ)(i)因为.files/image549.gif) ,
,
所以.files/image551.gif) ,即
,即.files/image553.gif) ,
,
.files/image555.gif) ,即
,即.files/image557.gif) . ……………………………………(6分)
. ……………………………………(6分)
因为.files/image559.gif) ,
,
当.files/image561.gif) 时,
时,.files/image563.gif) ,
,
当.files/image565.gif) 时,
时,.files/image567.gif) ,
,
所以.files/image569.gif) .
…………………………(8分)
.
…………………………(8分)
又因为.files/image571.gif) ,
,
所以令.files/image573.gif) ,则
,则.files/image575.gif)
得到.files/image577.gif) 与
与.files/image579.gif) 矛盾,所以
矛盾,所以.files/image581.gif) 不在数列
不在数列.files/image229.gif) 中. ………(9分)
中. ………(9分)
(ii)充分性:若存在整数.files/image243.gif) ,使
,使.files/image245.gif) .
.
设.files/image586.gif) 为数列
为数列.files/image237.gif) 中不同的两项,则
中不同的两项,则.files/image589.gif)
.files/image591.gif) .
.
又.files/image593.gif) 且
且.files/image243.gif) ,所以
,所以.files/image596.gif) .
.
即.files/image598.gif) 是数列
是数列.files/image237.gif) 的第
的第.files/image601.gif) 项. ……………………(10分)
项. ……………………(10分)
必要性:若数列.files/image237.gif) 中任意不同两项之和仍为数列
中任意不同两项之和仍为数列.files/image237.gif) 中的项,
中的项,
则.files/image605.gif) ,
,.files/image607.gif) ,(
,(.files/image609.gif) ,
,.files/image472.gif) 为互不相同的正整数)
为互不相同的正整数)
则.files/image612.gif) ,令
,令.files/image614.gif) ,
,
得到.files/image616.gif)
.files/image618.gif) ,
,
所以.files/image620.gif) ,令整数
,令整数.files/image622.gif) ,所以
,所以.files/image245.gif) . ……(11
分)
. ……(11
分)
下证整数.files/image243.gif)
若设整数.files/image626.gif) 则
则.files/image628.gif) .令
.令.files/image630.gif) ,
,
由题设取.files/image632.gif) 使
使.files/image634.gif)
即.files/image636.gif) ,所以
,所以.files/image638.gif)
即.files/image640.gif) 与
与.files/image642.gif) 相矛盾,所以
相矛盾,所以.files/image243.gif) .
.
综上, 数列.files/image237.gif) 中任意不同两项之和仍为数列
中任意不同两项之和仍为数列.files/image237.gif) 中的项的充要条件是存在整数
中的项的充要条件是存在整数.files/image243.gif) ,使
,使.files/image245.gif) .
……………………(14分)
.
……………………(14分)
21. (1)本题主要考查矩阵乘法、逆矩阵与变换等基本知识,考查运算求解能力, 满分7分.
解:.files/image649.gif) ,即
,即.files/image651.gif) ,
,
所以.files/image653.gif) 得
得.files/image655.gif) ……………………(4分)
……………………(4分)
即M=.files/image657.gif)
.files/image659.gif) ,由
,由.files/image661.gif) 得
得.files/image663.gif)
.files/image665.gif) .
.
或.files/image667.gif)
.files/image669.gif) =1
=1.files/image671.gif) ,
, .files/image673.gif)
.files/image665.gif) . …………………(7分)
. …………………(7分)
(2)本题主要考查圆极坐标方程和直线参数方程等基本知识,考查运算求解能力,考查化归与转化思想. 满分7分.
解:曲线.files/image148.gif) 的极坐标方程
的极坐标方程.files/image259.gif) 可化为
可化为.files/image678.gif) ,
,
其直角坐标方程为.files/image680.gif) ,即
,即.files/image682.gif) . ……………(2分)
. ……………(2分)
直线.files/image063.gif) 的方程为
的方程为.files/image685.gif) .
.
所以,圆心到直线.files/image063.gif) 的距离
的距离.files/image688.gif) ……………………(5分)
……………………(5分)
所以,.files/image690.gif) 的最小值为
的最小值为.files/image692.gif) .
…………………………(7分)
.
…………………………(7分)
(3)本题主要考查柯西不等式与不等式解法等基本知识,考查化归与转化思想. 满分7分.
解:由柯西不等式:
已知曲线.files/image694.gif)
 的极坐标方程是
的极坐标方程是 ,以极点为原点,极轴为
,以极点为原点,极轴为 轴正半轴,建立平面直角坐标系,两坐标系中取相同的长度单位.
轴正半轴,建立平面直角坐标系,两坐标系中取相同的长度单位.
(1)写出曲线 的普通方程,并说明它表示什么曲线;
的普通方程,并说明它表示什么曲线;
(2)过点
 作倾斜角为
作倾斜角为 的直线
的直线 与曲线
与曲线 相交于
相交于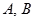 两点,求线段
两点,求线段 的长度和
的长度和 的值.
的值.
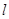 的极坐标方程是
的极坐标方程是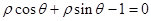 .以极点为平面直角坐标系的原点,极轴为
.以极点为平面直角坐标系的原点,极轴为 轴的正半轴,建立平面直角坐标系,在曲线
轴的正半轴,建立平面直角坐标系,在曲线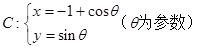 上求一点,使它到直线
上求一点,使它到直线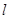 的距离最小,并求出该点坐标和最小距离
的距离最小,并求出该点坐标和最小距离 的极坐标方程是
的极坐标方程是 ,以极点为平面直角坐标系的原点,极轴为
,以极点为平面直角坐标系的原点,极轴为 轴的正半轴,建立平面直角坐标系,曲线
轴的正半轴,建立平面直角坐标系,曲线 的参数方程是:
的参数方程是: (
( 是参数).
是参数). 两点,求证
两点,求证 ;
; 交于两点
交于两点 ,且
,且 (
( 且
且 为常数),过弦
为常数),过弦 的中点
的中点 作平行于
作平行于 轴的直线交曲线
轴的直线交曲线 ,求证:
,求证: 的面积是定值.
的面积是定值. 的极坐标方程是
的极坐标方程是 .以极点为平面直角坐标系的原点,极轴为
.以极点为平面直角坐标系的原点,极轴为 轴的正半轴,建立平面直角坐标系,在曲线
轴的正半轴,建立平面直角坐标系,在曲线 上求一点,使它到直线
上求一点,使它到直线 的距离最小,并求出该点坐标和最小距离
的距离最小,并求出该点坐标和最小距离 的极坐标方程是
的极坐标方程是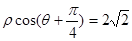 ,以极点为平面直角坐标系的原点,极轴为
,以极点为平面直角坐标系的原点,极轴为 轴的正半轴,建立平面直角坐标系,曲线
轴的正半轴,建立平面直角坐标系,曲线 的参数方程是:
的参数方程是: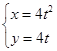 (
( 是参数).
是参数). 两点,求证
两点,求证 ;
; 交于两点
交于两点 ,且
,且 (
( 且
且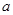 为常数),过弦
为常数),过弦 的中点
的中点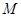 作平行于
作平行于 轴的直线交曲线
轴的直线交曲线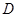 ,求证:
,求证: 的面积是定值.
的面积是定值.