（2013•房县模拟）问题：对于平面直角坐标系中的任意两点P₁（x₁，y₁）、P₂（x₂，y₂），我们把|x₁-x₂|+|y₁-y₂|叫做P₁、P₂两点间的直角距离，记作d（P₁，P₂）．如：P（-2，3）、Q（2，5）则P、Q两点的直角距离为d（P，Q）=|-2-2|+|3-5|=6
请根据根据以上阅读材料，解答下列问题：
（1）计算M（-2，7），N（-3，-5）的直角距离d（M，N）=．
（2）已知O为坐标原点，动点P（x，y）满足d（O，P）=1，则x与y之间满足的关系式为．
（3）设P₀（x₀，y₀）是一定点，Q（x，y）是直线y=ax+b上的动点，我们把d（P₀，Q）的最小值叫做P₀到直线y=ax+b的直角距离，试求点M（4，2）到直线y=x+2的直角距离．

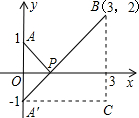阅读材料：
在直角坐标系中，已知平面内A（x₁，y₂）、B（x₁，y₂）两点坐标，则A、B两点之间的距离等于

(x2-x2)2(y2-y1)2

．
例：说明代数式

x2+1

+

(x-3)2+4

的几何意义，并求它的最小值．
解：

x2+1

+

(x-3)2+4

=

(x-0)2+(0-1)2

+

(x-3)2+(0-2)2

，如图，建立平面直角坐标系，点P（x，0）是x轴上一点，则

(x-0)2+(0-1)2

可以看成点P与点A（0，1）的距离，

(x-3)2+(0-2)2

可以看成点P与点B（3，2）的距离，所以原代数式的值可以看成线段PA与PB长度之和，它的最小值就是PA+PB的最小值．
设点A关于x轴的对称点为A′，则PA=PA′，因此，求PA+PB的最小值，只需求PA′+PB的最小值，而点A′、B间的直线段距离最短，所以PA′+PB的最小值为线段A′B的长度．为此，构造直角三角形A′CB，因为A′C=，CB=，所以A′B=，即原式的最小值为．
根据以上阅读材料，解答下列问题：
（1）完成上述填空．
（2）代数式

(x-i)2+1

+

(x-2)2+9

的值可以看成平面直角坐标系中点P（x，0）与点A（1，1）、点B的距离之和．（填写点B的坐标）
（3）求代数式

x2+49

+

x2-12x+37

的最小值．（画图计算）