摘要：图象如图代13-3-26.(3)解:由勾股定理.可知△CMA为Rt△.且∠CMA=Rt∠.∴MC为△CMA外接圆直径.∵P在上.可设.由MC为△CMA外接圆的直径.P在这个圆上.∴ ∠CPM=Rt∠.过P分别作PN⊥y.轴于N.PQ⊥x轴于R.过M作MS⊥y轴于S.MS的延长线与PR的延长线交于点Q.由勾股定理.有.即...而 .∴ .即 .∴ ..∴ .而n2=-2即是M点的横坐标.与题意不合.应舍去.∴ .此时 .∴P点坐标为.
网址：http://m.1010jiajiao.com/timu_id_6272[举报]
如图是2011年12月份的日历，小明同学在日历纵列上圈出了（象如图形式）三个数，算出它们的和，其中一个错误的是 （ ）
|
查看习题详情和答案>>
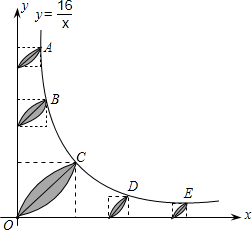已知，A、B、C、D、E是反比例函数y=| 16 | x |
13π-26
13π-26
（用含π的代数式表示）．
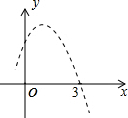（2012•苏州模拟）若二次函数y=-ax2+2ax+3的部分图象如图所示，则一元二次方程-ax2+2ax+3=0的根为