摘要：二次函数.若要使函数值永远小于零.则自变量x的取值范围是 A．X取任何实数 B.x<0 C.x>0 D.x<0或x>0
网址：http://m.1010jiajiao.com/timu_id_6197[举报]
下列表格是二次函数y=ax2 + b x +c的自变量x与函数值y的对应值，判断方程ax2+bx +c =0（a≠0,a、b、c为常数）的一个解x得范围是
[ ]
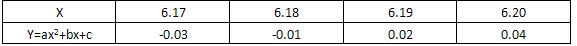
A.6 <x <6.17
B.6.17 <x <6.18
C.6.18 <x<6.19
D.6.19 <x<6.20
查看习题详情和答案>>
B.6.17 <x <6.18
C.6.18 <x<6.19
D.6.19 <x<6.20
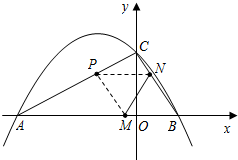如图，抛物线y=ax2+bx+c（a≠0）与x轴交于A（-3，0）、B两点，与y轴相交于点C（0，| 3 |
（1）求抛物线的解析式；
（2）若点M、N时从B点出发，均以每秒1个单位长度的速度分别沿BA、BC边运动，其中一个点到达终点时，另一点也随之停止运动．当运动时间为t秒时，连接MN，将△BMN沿MN翻折，B点恰好落在AC边上的P处，求t的值及点P的坐标；
（3）抛物线对称轴上是否存在一点F，使得△ACF是等腰三角形？若不存在请说明理由；若存在，请求出F点坐标．
请阅读下面材料：
若A（x1，y0），B（x2，y0） 是抛物线y=ax2+bx+c（a≠0）上不同的两点，证明直线x=
为此抛物线的对称轴．
有一种方法证明如下：
①②
证明：∵A（x1，y0），B（x2，y0） 是抛物线y=ax2+bx+c（a≠0）上不同的两点
∴
且 x1≠x2．
①-②得 a（x12-x22）+b（x1-x2）=0．
∴（x1-x2）[a（x1+x2）+b]=0．
∴x1+x2=-
又∵抛物线y=ax2+bx+c（a≠0）的对称轴为x=-
，
∴直线x=
为此抛物线的对称轴．
（1）反之，如果M（x1，y1），N（x2，y2） 是抛物线y=ax2+bx+c（a≠0）上不同的两点，直线x=
为该抛物线的对称轴，那么自变量取x1，x2时函数值相等吗？写出你的猜想，并参考上述方法写出证明过程；
（2）利用以上结论解答下面问题：
已知二次函数y=x2+bx-1当x=4时的函数值与x=2007时的函数值相等，求x=2012时的函数值． 查看习题详情和答案>>
若A（x1，y0），B（x2，y0） 是抛物线y=ax2+bx+c（a≠0）上不同的两点，证明直线x=
| x1+x2 |
| 2 |
有一种方法证明如下：
①②
证明：∵A（x1，y0），B（x2，y0） 是抛物线y=ax2+bx+c（a≠0）上不同的两点
∴
|
①-②得 a（x12-x22）+b（x1-x2）=0．
∴（x1-x2）[a（x1+x2）+b]=0．
∴x1+x2=-
| b |
| a |
又∵抛物线y=ax2+bx+c（a≠0）的对称轴为x=-
| b |
| 2a |
∴直线x=
| x1+x2 |
| 2 |
（1）反之，如果M（x1，y1），N（x2，y2） 是抛物线y=ax2+bx+c（a≠0）上不同的两点，直线x=
| x1+x2 |
| 2 |
（2）利用以上结论解答下面问题：
已知二次函数y=x2+bx-1当x=4时的函数值与x=2007时的函数值相等，求x=2012时的函数值． 查看习题详情和答案>>
如图，抛物线y=ax2+bx+c（a≠0）与x轴交于A（-3，0）、B两点，与y轴交于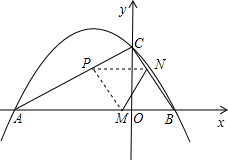
点C(0，
)，当x=-4和x=2时，二次函数y=ax2+bx+c（a≠0）的函数值y相等，连接AC、BC．
（1）求实数a，b，c的值；
（2）若点M、N同时从B点出发，均以每秒1个单位长度的速度分别沿BA、BC边运动，其中一个点到达终点时，另一点也随之停止运动，当运动时间为t秒时，连接MN，将△BMN沿MN翻折，B点恰好落在AC边上的P处，求t的值及点P的坐标；
（3）在（2）的条件下，抛物线的对称轴上是否存在点Q，使得以B，N，Q为顶点的三角形与△ABC相似？若存在，请求出点Q的坐标；若不存在，请说明理由． 查看习题详情和答案>>
点C(0，| 3 |
（1）求实数a，b，c的值；
（2）若点M、N同时从B点出发，均以每秒1个单位长度的速度分别沿BA、BC边运动，其中一个点到达终点时，另一点也随之停止运动，当运动时间为t秒时，连接MN，将△BMN沿MN翻折，B点恰好落在AC边上的P处，求t的值及点P的坐标；
（3）在（2）的条件下，抛物线的对称轴上是否存在点Q，使得以B，N，Q为顶点的三角形与△ABC相似？若存在，请求出点Q的坐标；若不存在，请说明理由． 查看习题详情和答案>>