摘要：点P在曲线C:上.若存在过点P的直线与C的两个交点为=
网址：http://m.1010jiajiao.com/timu_id_58931[举报]
点P在曲线C：
+y2=1上，若存在过P的直线交曲线C于A点，交直线l：x=4于B点，满足|PA|=|PB|或|PA|=|AB|，则称点P为“H点”，那么下列结论正确的是（ ）
| x2 |
| 4 |
| A、曲线C上的所有点都是“H点” |
| B、曲线C上仅有有限个点是“H点” |
| C、曲线C上的所有点都不是“H点” |
| D、曲线C上有无穷多个点（但不是所有的点）是“H点” |
点P到x轴的距离比它到点（0，1）的距离小1，称点P的轨迹为曲线C，点M为直线l：y=-m （m＞0）上任意一点，过点M作曲线C的两条切线MA，MB，切点分别为A，B．
（1）求曲线C的轨迹方程；
（2）当M的坐标为（0，-l）时，求过M，A，B三点的圆的标准方程，并判断直线l与此圆的位置关系；
（3）当m变化时，试探究直线l上是否存在点M，使MA⊥MB？若存在，有几个这样的点，若不存在，请说明理由．
查看习题详情和答案>>
（1）求曲线C的轨迹方程；
（2）当M的坐标为（0，-l）时，求过M，A，B三点的圆的标准方程，并判断直线l与此圆的位置关系；
（3）当m变化时，试探究直线l上是否存在点M，使MA⊥MB？若存在，有几个这样的点，若不存在，请说明理由．
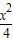+y2=1上，若存在过P的直线交曲线C于A点，交直线l：x=4于B点，满足|PA|=|PB|或|PA|=|AB|，则称点P为“H点”，那么下列结论正确的是（ ）